Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8N04
Numeracy Progression: Additive strategies: P10, Multiplicative strategies: P10, Number and place value: P9, Interpreting fractions: P9
At this level, students should be confident using the four operations to solve problems with integers and rational numbers. They can use a range of written strategies and mental computation to demonstrate their understanding.
Students look for patterns, recall number facts and laws, and choose efficient strategies to solve problems. When multiplying and dividing integers, students consolidate rules: the product of a positive integer and a negative integer is negative; the product of two positive integers is positive; and the product of two negative integers is positive. Students will need to revise the fraction arithmetic they learnt in the previous level and apply the rules of negatives.
When given a worded or contextualised problem, students identify the correct operations needed. It is important to provide opportunities to practise estimating with rational numbers, as this is an important skill.
Emphasise the importance of estimating to ensure that the answer found using digital technology is accurate. By this level, students should be able to handle calculations involving all elements of BIDMAS (Brackets, Indices, Division, Multiplication, Addition, Subtraction) with a combination of fractions and integers. Students can practise estimating rational numbers by rounding to the nearest whole number to get a clearer understanding of what the answer might be. Fractions can also be rounded to the nearest common fraction.
Allow students to continue to experiment with digital tools and interactives. Provide a range of contexts to deepen student learning and encourage the use of appropriate computations and representations. However, students should use digital tools where appropriate. This will depend on the computational abilities of each student, and they should be encouraged to use digital tools when mental strategies are ineffective or not appropriate.
It is useful for students to experiment with different kinds of calculators, including standard computer or phone apps and a scientific calculator. Even search engines can be used as calculators if using the correct syntax.
Teaching and learning summary:
- Revise and extend students’ knowledge of strategies for all operations of integers and rational numbers.
- Revise and extend students’ knowledge of strategies for multiplication and division of integers and rational numbers.
- Revise and consolidate calculations with fractions.
- Discuss estimation techniques for checking the reasonableness of solutions.
- Present students with contextualised problems where they can apply their knowledge and skills with the four operations by choosing the most efficient strategy and correct representations of number for that context. Translate worded problems into mathematical sentences.
- Practise using a range of digital tools, including those that students are likely to engage with regularly in their daily lives.
- Discuss the contexts in which technology may be more effective than mental strategies.
Students:
- know a range of mental and written strategies for solving problems with integers and rational numbers using the four operations
- identify the correct operation(s) to use when solving a contextualised problem
- make estimates, before calculating a solution, to assess the reasonableness of their solution
- follow the order of operations with a mix of rational numbers and operations
- identify whether a mental or digital strategy is most appropriate in a given context.
Students may:
- think that adding a number always increases and subtracting a number always decreases.
- subtract numerals and then attempt to determine the sign for the answer.
- not align the decimal point correctly when using column arithmetic.
- forget to use zeros as placeholders when adding and subtracting decimals.
- struggle with addition of fractions with unlike denominators, as well as multiplication and division of fractions.
- have used a variety of different order of operations acronyms depending on the primary school they attended.
- find it difficult to translate worded problems into mathematics.
- use a calculator and associate being poor at mental and written calculations with being poor at mathematics.
Misconceptions that students may hold when operating with number and how to address them are also found at this resource.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I am learning to apply the four operations to rational numbers in any order.
- I can make sensible decisions about when to estimate or calculate exactly, and when to use digital tools.
Why are we learning this?
From cooking to budgeting, calculations are a regular part of our daily life. Although we often rely on technology nowadays, it is still useful to be able to perform calculations quickly in our head. It’s not always more efficient to turn to our phones or computers. Plus, it’s healthy for our brains to get a regular workout.
What to do
You have now practised all four operations with whole numbers and fractions and know the correct order to follow when multiple operations are involved. It’s time to show off those skills.
- Grab a blank piece of paper and a pencil and find someone in your house who you’d like to impress. Ask them to write down a complicated arithmetic problem for you, with any numbers and operations they like; the more the better. Encourage them to use fractions and negative numbers too.
- You don’t always have to try to calculate the exact answer. If you have been given a problem with overly complex numbers, round them! Instead of 875 × 29 use 900 × 30, instead of 3473 use 12. You will impress with how fast you were able to do the calculation while maintaining such a high level of accuracy!
- Show your working out and explain the choices you made and why it was appropriate to round in complicated cases – thinking is more valuable than simply computing mindlessly.
- Generate some more of these questions for yourself. Throw a few numbers and symbols onto the page and have a go. Test out your calculator skills when you verify your solutions.
- Each time you find a problem that you are confident you can do by hand, solve the same problem using mental strategies first, and time how long it takes you.
- Then observe how much time you can save by estimating the same problem. How much accuracy did you lose?
- Use your calculator to check how close you were to the exact answer. Try it again but round only the tricky numbers first.
- How much faster were you? How much accuracy did you lose?
Success criteria
- I am confident about tackling problems involving any operations, with any rational numbers, in any order.
- I can make sensible decisions about when to estimate or calculate exactly, and when to use digital tools.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Shooting 3-pointers: Part 1
In this lesson students are guided through solving a problem using mathematical modelling.
Go to resource -

Shooting 3-pointers: Part 2
In this lesson, students conduct a statistical investigation.
Go to resource -
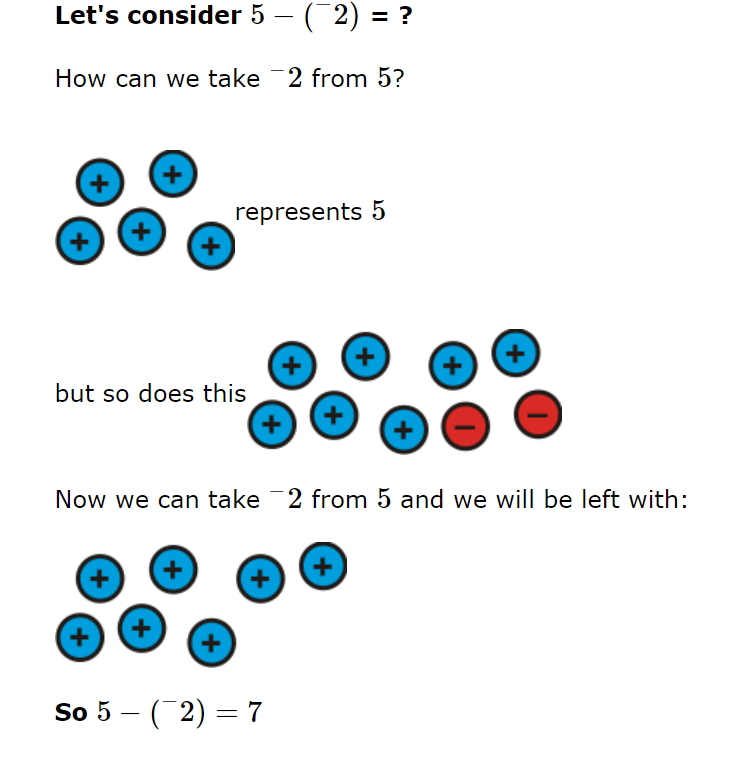
Adding and subtracting positive and negative numbers
Students are taught how to add and subtract positive and negative numbers using various models presented.
Go to resource -

Whole number arithmetic
This teacher guide covers explanatory notes, worked examples and sample questions around how students use the four operations, providing mental strategies to complement formal arithmetic.
Go to resource