Addition and subtraction: Year 7: Planning tool

Expected level of development

Australian Curriculum Mathematics V9: AC9M7N07

Numeracy Progression: Additive strategies: P10, Number and place value: P9

At this level, students compare, order and solve problems involving addition and subtraction of integers. Brainstorm with students the different techniques and strategies used to solve addition or subtraction problems. Students can reflect by ordering the strategies from their most to least favourite technique.

Revise associative and commutative laws to help students make mental computations easier and to make reasonable estimates. Explain that the commutative and associative laws only apply to addition and multiplication and not for subtraction and division, and demonstrate why this is the case. Using number lines is a good way of illustrating this.

The Concrete Representational Abstract model is a good way of developing students’ understanding of these properties. Use physical objects, such as counters, and drawing representations, such as arrays, to enable students to make sense of the abstract notation we use in mathematics.

Students begin to operate with negative integers. This is a concept students often struggle with and time should be taken to explain and demonstrate the concepts in a variety of ways, such as using double-sided counters. Make connections with
< (less than) and > (greater than) signs between various integers so that students can visualise and make comparisons. This can be done visually with number lines, or a vertical number line representing the floors of a skyscraper.

Cement the understanding of the + sign as moving to the right and the – sign as moving to the left, with the first value representing the starting position and the second value representing the number of steps. Consolidate the concept that adding a negative is the same as subtracting a positive and that subtracting a negative is the same as adding a positive. Convey this with gestures – a horizontal finger on each hand representing a minus sign can be brought together to make a plus. A minus always overpowers a plus, so when you see both next to each other, the minus kicks out the plus.

Diagrams are helpful here too. In X + Y or X – Y, X is the starting position, the + or – sign is the direction of travel along the number line, and Y is the number of steps.

Demonstrate the value of ordering and rearranging. Increase depth of understanding by using real-life scenarios, for example, paying for items at a cash register or comparing temperature changes. Encourage students to use estimation as a way of determining reasonable answers, especially when using calculators and other technology.

Having a good knowledge of these concepts provides scaffolding for students to manipulate algebraic expressions.

Practise these steps in the order given:

Positive number: subtract a positive number, to get a negative solution.
Negative number: add a positive number, to get both negative and positive solutions.
Positive number: add a negative number, to get both negative and positive solutions.
Negative number: add a negative number, to get both negative and positive solutions.
Positive number: subtract a negative number.
Negative number: subtract a negative number, to get both positive and negative solutions.

Teaching and learning summary:

Demonstrate the associative and commutative rules and how they can aid mental computation.
Encourage students to use estimation as a check that a solution is reasonable.
Revise the concept of negative integers and where they are on a number line.
Introduce operations with negative integers.
Compare, order and rearrange integers in numerical calculations and for worded problems.
Use a variety of vocabulary so that students can solve problems.
Revise a range of arithmetic strategies.
Identify the role of each element in a calculation.
Use scaffolding to build up to the more complex calculations involving negative integers.

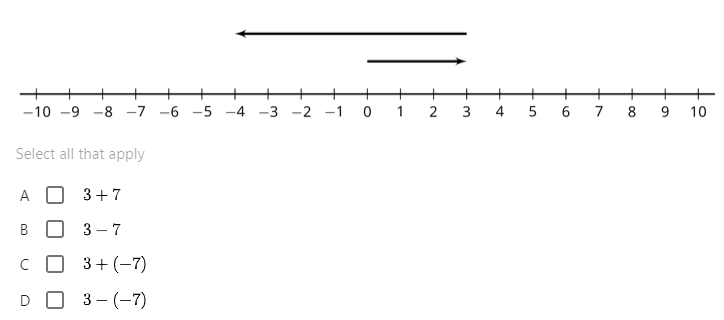
Students:

understand the associative and commutative properties
are able to apply these properties to simplify mental calculations
correctly place positive and negative integers on an extended number line
draw on real-world examples of negative numbers
are able to compare, order and solve problems involving addition and subtraction of integers
recognise a range of vocabulary around addition and subtraction and can solve problems choosing the correct magnitude and operation of integers.

Some students may:

confuse signs for greater than and less than (the hungry crocodile always eats the bigger number).
not be aware of the properties of the associative, commutative and distributive laws and use them incorrectly for mental and written computation.
use the commutative and associative rules to subtract and divide computation.
use the language of addition and subtraction of positive and negative numbers incorrectly, that is, ‘two minuses make a plus’ to calculate.
not know of other strategies other than 'doing it in my head'.
not know the role of each element in a calculation.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

Apply your understanding of positive and negative numbers and the laws to complete mental and written problems.
Efficiently add and subtract positive and negative integers to win a game against your family and friends.

Why are we learning about this?

Learning about positive and negative numbers is important as there are so many instances in life where they are used. For example, taking the elevator below ground level is indicated by negative numbers, while above ground is indicated by positive numbers. These skills are the foundation to success in the rest of secondary mathematics. Learning to count is like learning the alphabet. Learning to add and subtract is like learning how to write a sentence and spell words. We can’t do much else without it!

What to do

Get ready to race against your family or friends. You’ll need a deck of cards and a timer for this game, and a few simple rules:

Aces are special cards that activate a switch (addition switches to subtraction or subtraction switches back to addition).
Kings, Queens and Jacks count as 10.
Red cards are negative numbers.
Black cards are positive numbers.

To begin

Remove the jokers.
Shuffle the cards and deal them out evenly between all players. If four people are playing, each player will receive 13 cards. Keep your pile of cards face down.
Turn your top card over. This is your starting number. If your top card is an ace, you will begin on subtraction, everybody else begins with addition. You’ll need to turn over your next card for your starting number.
Start the timer and flip over the next card. This needs to be added or subtracted to your starting number. (Remember: black cards are positive numbers and red cards are negatives.)
Keep going until your pile is finished and don’t forget to switch if you see an ace.
Note down the time it took each player to finish and the number they finished on.
Check each player’s calculations by going back through their pile with a calculator. Your time will be increased by three seconds per number of errors. If you calculated 47, but the calculator says 50, you’ll be adding nine seconds to your time. Don’t rush!
The player with the fastest time wins the round.

Success criteria

I can place positive and negative numbers on a number line.
I can order, add and subtract integers using a number line.

Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.

Planning tool

Year levels

Strands

Topics