Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M7M06
Numeracy Progression: Understanding units of measurement: P8, Proportional thinking: P3
At this level, students apply the mathematical modelling process to solve practical problems involving ratios. This is a natural cross-curriculum link with Food Studies, Design and Science and teachers should consider consulting with those teaching teams during planning. Students can create a model to make predictions about the amount of solute required for a particular-sized solution, or the quantity of ingredients needed to scale-up a recipe.
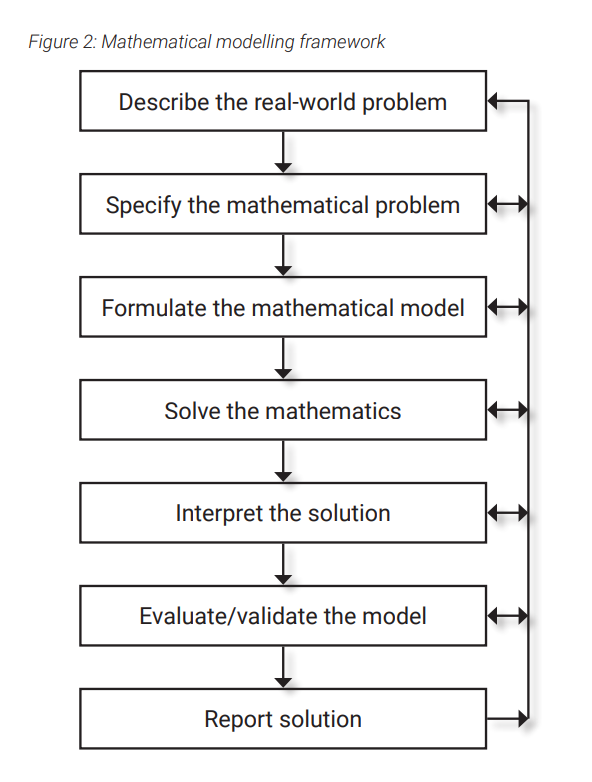
Illustrate to students that the modelling process uses mathematics to make predictions that help us to understand the world around us. The role of the teacher is key as students will require support at every step as they start to familiarise themselves with the modelling process.
Students must have a solid understanding of the problem they are trying to solve. Support students to ascertain the prediction they are trying to make, and the data and variables required to make the prediction. If necessary, the real-world context may need to be simplified by a set of appropriate assumptions. Help students to brainstorm a range of mathematical methods that can be used to solve the problem, exploring the advantages and drawbacks of each. Students must select one method and provide justification for their choice. Encourage students to reflect on whether they selected an appropriate model. Ensure students apply their chosen method correctly to generate a relevant prediction. Finally, students should communicate their prediction in context, evaluate its accuracy, highlight potential flaws in methodology and the reasoning behind their choices.
Heavy scaffolding is recommended before students attempt the process independently. Use worked examples of a completed process and work through a further scenario with students collaboratively. For example, allow students to move around the school to collect data to predict the total number of chairs, or heating/cooling vents in the school. Examples such as these require skills in sampling and to build a model ratio, demonstrating variance (depending on which rooms they choose to sample) to extrapolate the entire number of chairs in school.
Plan sufficient time for students to present their findings emphasising that modelling is a practical rather than a theoretical application of mathematics. This allows for effective communication of results to a wide audience. The focus of this task, however, is to not only solve the problem but to work through the process to solve the problem. That is to say, the process is the main learning goal, which will be revisited regularly.
Teaching and learning summary:
- Demonstrate and illustrate how the mathematical-modelling process can be used to solve real-world and practical problems.
- Explicitly teach a version of the process that students can apply repeatedly.
- Emphasise the opportunity for this process to be applied in a range of other learning areas.
- Gradually release the responsibility to students to use the process independently after first providing a worked example and then a whole-class activity.
- Encourage the need for creativity both in the way a problem is approached as well as how the predictions are presented.
- Highlight the importance of justifying and evaluating the selected methodology, and accompanying assumptions.
- Consider the fallibility of modelling and the need to be open to feedback, which can be reincorporated into the model to improve its predictive power.
Students:
- explain the purpose, strengths, and limitations of mathematical-modelling processes
- recall the steps of the chosen mathematical modelling process
- identify a real-world problem and understand it in context
- apply ratios and other mathematical methods of measurement to make predictions that help solve the identified problem
- use manipulatives or other representations to model the problem
- clearly communicate, evaluate, and justify choices and methods.
Some students may:
- miscalibrate the effectiveness of the mathematical-modelling process. It is important to reiterate that modelling uses current and past data to predict future events. It is therefore reliable, but fallible.
- not widely consider the context of a particular problem.
- be inclined to estimate or guess a solution rather than following the process. Students may not distinguish between modelling and guessing.
- have difficulty comparing different methodologies and justifying their choices. Students will likely revert to whichever mathematical techniques are easiest, or quickest, for them.
- have knowledge or skill gaps with ratios that need to be addressed first.
- have difficulty in formulating the correct equation or expression needed to solve the problem.
- Rush the communication and justification steps of the process as they may not associate them with mathematics learning.
Students develop a more complex mathematical skillset throughout the next several levels, they can create progressively more accurate and sophisticated models. The more complex a real-world scenario is, the more nuanced the model must be. This can help to build engagement for future topics such as polynomials and functions.
During the COVID pandemic, the importance of modelling became more central to all our lives. Teams of mathematicians worked hard to build models to predict how the virus would spread through the community. This kind of information is very useful to people who need to make decisions that affect many people. It is always better to make decisions based on evidence or data. While mathematical models are not always perfectly accurate, they increase the likelihood of making good decisions.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I will use the mathematical-modelling process to make a reasonable prediction to a challenging problem.
- I will use ratios as my mathematical method.
Why are we learning about this?
You have learnt how estimating can be a powerful tool to improve decision making. Using a mathematical-modelling process takes this to the next level by finetuning the predictive process to ensure a high likelihood of success. With a solid grasp of this process, you can make predictions that you are confident in.
What to do
How much does my local community recycle?
Recycling more of our waste is big challenge facing Australia over the next decade. Solving this problem will help us meet our climate goals. Wouldn’t it be interesting to know how good your local community is at recycling? Do you wonder how much recyclable waste is collected in your neighbourhood? If you can gather some accurate data on this, it might inspire a local awareness campaign that boosts the percentage even higher!
Your job is to determine an accurate ratio of recycled waste : landfill waste. Of course, you won’t be able to measure all the waste in your suburb, so you’ll need to be hyper-local.
- Over the course of a few weeks check the level of waste in the landfill and recycling bins of yours and your neighbours’ bins. Do this on the night before bin collection. In our house, it’s called ‘bin night’.
- You will need to ask your neighbours’ permission first. Explain the maths task you are working on and that you are collecting data to build a neighbourhood dataset.
- Tally up the total number of bins of recycled waste and landfill waste over this period. Remember, the more accurate your measurements, the more accurate your model!
For example, you may observe a total of 11.25 bins of recycled waste and 15.5 bins of landfill waste. This gives a ratio of 11.25:15.5. You might recall that decimals aren’t ideal in ratios, so multiply both sides by 4 to remove them. This gives us a ratio of 45:62 (recycled: landfill).
- Now you have a model ratio for recycling that you can use to predict the rate of recycling in your suburb.
- Consider whether your model needs refining? Do you think the model makes an accurate prediction for a larger group of households? Consider other questions.
- Did you include a diverse group of households in your sample data?
- Was it a particularly wasteful time of year (e.g. holidays or parties)?
- Are there different-sized bins within your council?
- Were there any other factors observed during this period?
- After considering these questions, adjust your model as you see fit.
- Now you are ready to predict how much waste is recycled in your neighbourhood. Convert your ratio in a percentage, and voila!
Extension
Make an impact with your model by communicating your findings to the local council in an aesthetically appealing form. You may even be featured in the local newsletter! Maybe you will inspire your neighbours to recycle more! You should include an evaluation of your model that justifies the choices you made when building and refining your model. Ensure you explain your methodology and reasons. Question whether there is council data you can compare to? If so, are they similar? Why or why not?
Success criteria
- I can use a mathematical-modelling process to evaluate a local service in my council area.
- I can model a real-world problem using ratios, communicate my prediction, and justify my choices.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Mathematical modelling: Pizza problem
In this lesson, students are provided with a real-world problem related to takeaway pizza where they gathering evidence as they investigate a claim.
Go to resource -
Teacher package: mathematical modelling
Numerous differentiated activities and ideas to bring mathematical modelling into the classroom.
Go to resource -
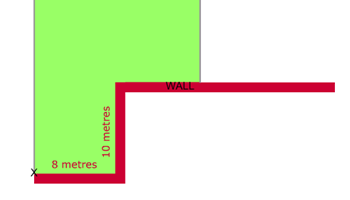
Fence it
What is the largest area you can fence given a length of fencing?
Go to resource -

Mixing paints
What ratio of red and white paint will give you the correct shade of pink?
Go to resource -

Old scales
Which three weights do you need to weigh any whole number of kilograms from 1kg to 13kg?
Go to resource