Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8M07
Numeracy Progression: Proportional thinking: P6, Interpreting fractions: P9
At this level, students build on their mathematical-modelling skills from the previous level using a mathematical-modelling process to solve problems related to ratios and rates. It is recommended to include financial contexts as part of their investigations for this topic.
Students build on their critical and creative thinking skills, interpreting aspects of a particular problem while recognising any missing elements that will allow them to choose appropriate mathematical processes to find solutions to their formulated problems. Students interpret and communicate their findings explaining the context as well as provide reasons for their method chosen. It is important for students to evaluate their process considering their solutions and to take this opportunity to argue their choices made.
Suggest varied real-world contexts for students to explore as part of their investigation, such as modelling ratio and its applications in the making of various tools by First Nations Australians, as recommended in the curriculum.
Financial contexts are also recommended and emphasised. As students begin thinking about their first part-time jobs, this presents an opportunity to consider rates such as hourly wages, superannuation, GST and income tax.
Investigations such as these present collaborative learning experiences by having students present various predictions based on differences in hourly wages at different workplaces and connecting this to the working hours required for spending or saving. Presenting a set of predictions, based on distinctly modelled rates provides an excellent opportunity for students to interpret the reasonableness of their solutions, and how appropriate each model is. Extend this investigation further and increase engagement by organising for students to interview Year 12s and ask questions about their financial positions. This real-world data can inform students and allow them to interpret and evaluate their own modelling.
While this task may be engaging for students, teachers should monitor to see that students do not get overly consumed and emphasise that the task should be designed to carefully reinforce the core mathematical-modelling process.
Teaching and learning summary:
- Reinforce how the mathematical-modelling process can be used to solve real-world and practical problems.
- Explicitly re-teach a version of the modelling process.
- Seek out opportunities for cross-curriculum collaboration, potentially with Economics and Business subject areas.
- Provide worked examples to model the process and heavily scaffold a whole-class activity before releasing students to attempt it independently.
- Explore students’ entry to the world of work and the myriad of associated rates.
- Encourage the need for clear, creative, and context-specific communication of their solution.
- Emphasise the need to interpret the prediction and any assumptions or simplifications built-in to the model.
- Understand the fallibility of modelling and the need to evaluate the appropriateness of the selected model. Seek feedback and data to confirm or reject the model’s effectiveness.

Students:
- explain the purpose, strengths, and limitations of the mathematical-modelling process
- recall the steps of the chosen mathematical-modelling process
- investigate financial contexts such as wages, tax rates and savings goals to predict students’ future financial positions
- access publicly available data to review the appropriateness of models
- communicate, evaluate, and justify the choices and methods chosen in the model.
Some students may:
- be unfamiliar with financial terms and concepts or have not considered the idea of earning, saving, and spending their own money.
- not understand that a rate is the comparison between two quantities with different units. Explicitly teach the correct use of the word ‘per’ and the forward slash symbol (/).
- incorrectly order the units in a rate.
- miscalibrate the effectiveness of mathematical modelling. It is important to reiterate that modelling uses current and past data to predict future events. It is therefore reliable, but fallible.
- be inclined to estimate or guess a solution rather than following the process. Students may not distinguish between modelling and guessing.
- have difficulty in formulating the correct equation or expression needed to solve the problem.
- rush the communication and justification steps of the process as they may not associate them with mathematics learning.
- be unsure how to review the appropriateness of a model that is predicting something in the future.
Encourage a variety of contexts that are authentic to students so that they can connect with modelling process. Suggest contexts from other disciplines, such as economics and business, health and physical education. Consider using First Nations contexts.
Examples of an extended investigation could be constructed that helps students to plan large purchases (for instance, their first car) by modelling how much money can be earnt between now and then; how much is required to be saved; and therefore, how much they can freely spend with the remainder. This investigation could involve researching prices on the second-hand car market – considering how the price of a newer car might inflate over the coming years or how older cars will depreciate.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I will apply the mathematical-modelling process to predict the cost of post-graduation backpacking trip.
- I will interpret and communicate my findings and explain the choices made in my mathematical-modelling process.
Why are we learning about this?
Now that we are familiar with the modelling process it’s time to expand our horizons. Modelling can be used to inform both short- and long-term decision-making. Forming a plan many years in advance may seem a little strange at first. But, if we model the long-term future, it can help us to set realistic goals, or adjust our plans to make big dreams a reality.
What to do
Plan a backpacking adventure!
- Got a dream route in mind? Map out where you’d like to go backpacking, and for how long, after you successfully complete
high school. - Consult travel websites to find the cost per day of the cities on your list. For example visit the United Nations World Tourism Organization to gather your data.
- Convert the daily rates into $AUD.
- Adjust for inflation. You won’t be taking this trip for another five years so it’s highly likely that prices will rise. By how much though? You’ll need to find publicly available data that tracks inflation. This is where you have options, and they could affect the appropriateness of your model. Consider the following but remember, whichever choices you make, be sure you know why you’ve made them. You should explain these at the end.
- Do you use a conservative or optimistic prediction of future inflation?
- Will you find separate inflation data for each country?
- Will you base it on regional data, or world averages?
- (Optional) If you’re keen for more planning, map out the flights you need to take and research the cost (adjusted for inflation) for these.
- Calculate your total predicted cost by combining the length of your stay in each city with your inflation-adjusted, $AUD rates.
- (Optional) Summarise your findings in a graphic that you can display in your room for motivation!
- Review the appropriateness of your model. What choices did you make earlier? How may these affect the eventual accuracy of your predicted cost? Are there other factors you could have considered? Have other similar models been produced that you can find online for comparison?
Success criteria
- I can use rates in a financial context to generate a mathematical model that solves a practical problem in my future.
- I can evaluate and consider the appropriateness of my model and explain my reasoning behind its design while thinking about other factors I could have considered.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Culturally responsive pedagogies
Mathematics is not an exclusive western construct. Therefore, it is important to acknowledge and demonstrate the mathematics to be found in all cultures.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Solving problems involving rates and ratios
A teaching resource on how to teach ratios and rates. Includes activities.
Go to resource -

Recognise and solve problems involving simple ratios
Students can work individually or in groups to complete each real-world scenario.
Go to resource -
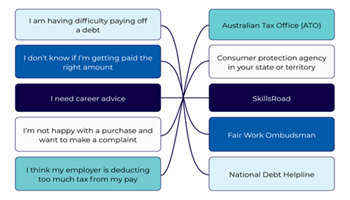
Different ways to pay
Students learn about the pros and cons of various payment options, what happens to their money, different consumer products and where to go for more information.
Go to resource
Assessment
By the end of Year 8, students can use mathematical modelling to solve practical problems involving ratios and rates, including financial contexts. Students can formulate problems, interpret and communicate solutions and review the appropriateness of the model.
-

Mixing lemonade
This problem investigates fractions, ratio and proportion. Students compare fractions or ratios while thinking about which strategies are most useful for different cases.
Go to resource -

Body ratios
Students can apply a mathematical-modelling approach to solve problems on rates and proportion.
Go to resource -

Comparing by finding rates
Students solve problems using a mathematical-modelling approach.
Go to resource -

WS3 - Design a putt putt course | V9 Australian Curriculum
Use this task to guide assessment of students’ proficiency in using mathematical modelling to solve a practical problem involving measurement.
Go to resource