Planning tool

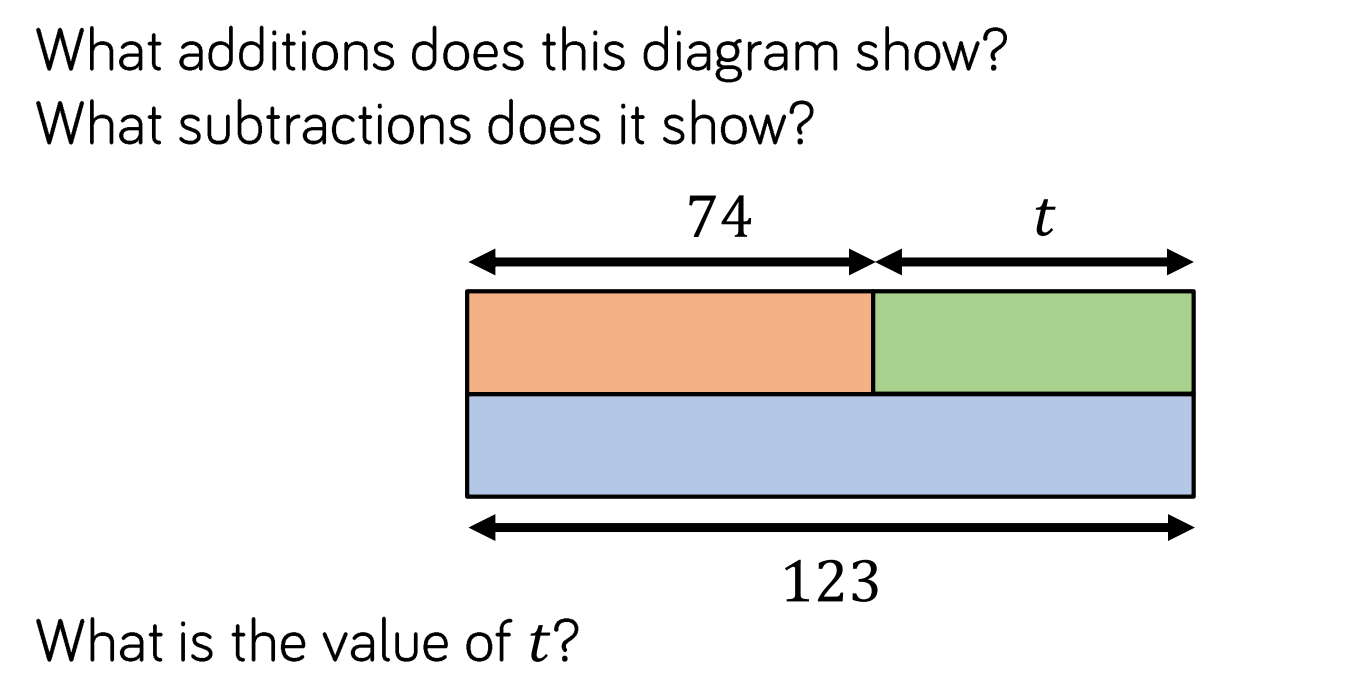
Students:

• write an expression or equation from a word problem using pronumerals
• substitute a value for a pronumeral into an expression (or formula)
• manipulate pronumerals in expressions mathematically
• solve two-step equations with variables on one side.

Some students may:

• try to guess the answers to simple equations but then find more complicated equations difficult when guessing is not possible.
• not realise that pronumerals are standing in place of a number.
• confuse the variable x with the multiplication symbol.
• not respect the ‘grammar’ of mathematics – algebra is a language with its own rules of grammar and there is a specific way to ‘read’ or ‘write’ an expression.
• think that 3x + 2x = 5x². To address this, be very specific with your language when reading expressions and equations. Say: ‘three lots of x is added to two lots of x to give a total of five lots of x’. And that 5x² should be said as ‘five lots of x squared’.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

• We are learning how equations were first used to solve important everyday challenges.
• We are learning how to solve linear equations.

Why are we learning about this?

Being able to solve equations makes us much more powerful mathematicians. If we want to use mathematics to answer important questions, we will first need to solve an equation. In finding the answer to our equation, we will find the answer to our real-world question. We begin with simple equations that you might be able to solve simply by looking at them. But wait, not so fast! Equations can become much more complicated. We are starting here to sharpen our skills so that we can use them to solve more difficult equations.

What to do

Part A

We are going to transport ourselves to an ancient, bustling marketplace. There are lots of colours, smells and noises. In some ways it is very similar to the markets you might be used to in our world of today, but there are some important differences. We have some nifty tools at our disposal such as our modern scales. Let us imagine a marketplace we have seen before, but without any of its modern technology.

You will need the following:

• produce from your fridge or pantry to sell – something that does not state its weight, for example, a strawberry, a lettuce leaf or some grapes
• balance scales, for example, old kitchen scales, or borrow some at school
• weights, for example, M&Ms, Smarties, dried beans or black peppercorns – something that you have lots of, and are all the same shape and size.

A customer (maybe one of your siblings or friends) comes along and asks to buy some of your grapes. They have a budget of 30 Smarties, so they plonk down their 30 Smarties on one side of your scales and start filling the other side with your grapes.

But the grapes and Smarties do not balance evenly because 7 grapes are too light and 8 are too heavy. What can you do?

You add a couple Smarties to the side of the scales with the 7 grapes until it balances perfectly. Now you have a Babylonian equation.

7g + 2 = 30

On the scales there are 7 grapes and 2 Smarties on one side and 30 Smarties on the other. This means your customer will receive 2 Smarties as change plus their 7 grapes.

Part B

Your customer wants to know how much they paid per grape. An important question that we can only answer by solving our equation above. Let’s work it out in steps.

1. 7g + 2 = 30; we subtract 2 from both sides to ‘undo’ the +2
2. 7g = 28; we divide both sides by 7 to ‘undo’ the ×7.
3. g = 4; so each grape cost 4 Smarties.

Now it is your turn to create your own equations that you solve from the transactions at your market stall.

Hint: place a set amount of weight on one side of the scales and then place a combination of produce and weights on the other until they balance. Never remove a weight.

Here is another example to guide you:

• 3 cherry tomatoes and 4 weights on one side and 25 weights on the other.

3t + 4 = 25

∴ t = 7

Extension task A

Try putting produce on both sides of your scales. This will make your equations more complex. For example, 3 cucumbers and 20 weights on one side and 5 cucumbers and two weights on the other.

3c + 20 = 5c + 2

How can we solve this? The best strategy would be to remove the 3 cucumbers on the left and remove 3 cucumbers from the right. Mathematically, we have subtracted 3c from each side of the equation. Our equation is now:

20 = 2c + 2

You already know how to solve that. Did you find that each cucumber must weigh 9 units?

Extension task B

You might have noticed that in your market stall all the equations looked quite similar and had to be solved in the same way; that is, you needed to subtract a number from both sides and then divide both sides by a number.

To extend our skills, we need to practise with a variety of equations.

Try to solve the equations below using the same technique, but keep in mind that you will not always be subtracting and dividing, you might need to apply a different set of operations.

Success criteria

• I can generate and solve equations that model real-world scenarios.
• I can ‘undo’ all four operations in the correct order.