Expected level of development
Australian Curriculum Mathematics V9: AC9M8A01
Numeracy Progression: Number patterns and algebraic thinking: P7
At this level, students build on their knowledge of the order of operations, simplifying algebraic terms and their prior knowledge of the arithmetic laws. Students will now create and rearrange linear expressions, as well as expand and factorise them.
Revision of the associative, commutative, identity, distributive and inverse properties and laws is important grounding in this topic. For example:
- 2x + 12 = 2(x + 6)
- 4(a – b) = 4a – 4b
- 3(m +2n) + 2m – 3n = 3m + 6n + 2m – 3n = 5m + 3n
Algebraic terms, such as ‘like terms’, should be clearly explained. Use the language of algebra regardless of your explanatory approaches, so that students know that different methods of approaching problems are related to the same concepts. Reinforce the properties of ‘terms’ especially when they are negatively signed (e.g. –3g), so that students find rearranging equations easier.
The area model is a visual method for explaining the distributive law and the process of expanding expressions. Using concrete (or virtual) manipulatives such as algebra tiles will develop students’ conceptual understanding of expanding brackets. The same approach can be used when extending learning to negative terms, binomial expansion and factorising, thus making the links between binomial expansion and factoring clear.
At this level, students continue to develop their knowledge of algebraic expressions and their understanding that the laws used with numbers, such as the associative and commutative properties, also apply to algebra.
Making the link between algebra as a distinct concept and its use in all areas of mathematics (and beyond) will support students to see the relevance and importance of this topic. For example, demonstrating how algebra is used in measurement: writing an expression for the perimeter of a shape, or an equation when finding a dimension given the area of a square.
Teaching and learning summary:
- Review the associative, commutative, distributive, identity and inverse properties and laws.
- Revise previous knowledge of pronumerals and coefficients.
- Explain the label ‘like terms’ and how to simplify expressions.
- Demonstrate the relationship between expanding and factorising expressions.
- Demonstrate the process for expanding expressions.
- Use manipulatives like algebra tiles and area models to model algebra problems.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
We are learning the connection between algebraic expressions and areas of shapes.
Why are we learning about this?
We learn how to add, subtract, multiply and divide because these are important number skills that come in handy all the time. Numbers are concrete and help us with things we can count or measure, whereas algebraic expressions are variable, and can help us with things we don’t know – or can’t easily find – the answer to. So, we need to be able to implement their operations correctly. Expanding, factorising, rearranging and simplifying might not sound as familiar, but they are as equally useful as their numerical cousins.
What to do
1. Draw two rectangles with the same width but different lengths. Here’s an example below.
2. Assign measurements to each of their dimensions. Like this.
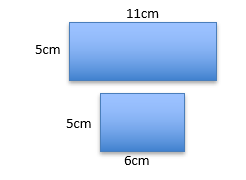
3. Can you calculate the total area of the rectangles? Write down all of your workings.
I’m going to guess that you did something like 55 + 30 = 85cm2. If you did, that’s absolutely correct. But there’s an even cleverer way! Let’s line the rectangles up, side by side, like so.
Now we have one large rectangle instead of two smaller ones.
Width = 5cm
Length = (11 + 6)cm
To calculate the area we will still take the product of the width and length: 5 (11 + 6).
Notice how I have left out the multiplication sign between them. You should recall that we are allowed to do this when we have a number next to parentheses or a pronumeral. The expression above is ‘factorised’ because it has a common factor removed from each of the two rectangles – the common width of 5cm.
If I multiply each of the separate lengths by the width, we return to the previous expression of 55 + 30. This is called an ‘expanded’ expression. It no longer clearly shows us what is common between the two rectangles.
In fact, it is possible that the first rectangle is 22.5cm long and 2cm and the second might be 10cm long and 3cm wide. We receive less information from the expanded expression.
4. Can you repeat this process with new pairs of rectangles?
5. Write down both an ‘expanded’ and ‘factorised’ expression for their combined areas.
6. Now you can try with three, four or even five rectangles. What changes in your expressions?
Challenge
Let’s return to pairs of rectangles. We still want them to share a common width, but now I’d like you to only label one of the lengths and assign a variable to the other. It might look like this:
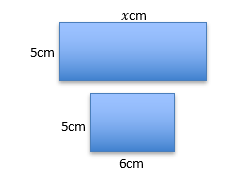
7. Can you write the factorised and expanded expressions for the areas of these rectangles?
8. What do you notice?
It’s a little easier to spot the usefulness of this technique once we apply variables. Try a few of your own pairs of rectangles, and then experiment with more than two. You might even add more variables.
Extension
Take one of your expressions for the area of two rectangles (with a variable) and set it equal to a value.
9. Can you solve the equation?
10. If that value was the total area, what is the missing length?
11. Did you pick a large enough value for the total area?
12. If not, how can you predict this before selecting?
Success criteria
- I can distinguish between factorised and expanded expressions and convert between them.
- I can represent algebraic expressions as sets of rectangles.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Working with algebra
This resource includes three separate activities that consolidate the core algebra skills of operating with and manipulating algebraic expressions.
Go to resource -
Number and algebra
From the AMSI Supporting Australian Mathematics Project, this resource gives detailed explanations for teachers and students of the curriculum content, worked examples and assessment questions. This resource focuses on how to expand brackets, simplify and factorise algebraic expressions.
Go to resource -
Think of a number
This resource consists of puzzles where students must balance the sides of a mobile. Done using shapes and colours, the puzzles get progressively more complex, and make a great lesson starter. Teachers can also create their own puzzles.
Go to resource -
Patterns and algebra
This resource discusses how the proficiencies can be embedded into teaching pattern and algebra by using practical, contextualised examples. For each activity there is a section on content knowledge, question ideas and responses, extensions and connections to other curriculum areas.
Go to resource
Assessment
By the end of Year 8, students can apply algebraic properties to rearrange, expand and factorise linear expressions. Students can use associative, communicative, identity and distributive laws and inverse properties.
-
Number and algebra
From the AMSI Supporting Australian Mathematics Project, this resource gives detailed explanations for teachers and students of the curriculum content, worked examples and assessment questions. This resource focuses on how to expand brackets, simplify and factorise algebraic expressions.
Go to resource