Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M6P01
Numeracy Progression: Understanding chance: progression: P4, Proportional thinking: P1
At this level, students represent the probability of an event occurring on a scale of zero to one as decimals, fractions or percentages.
Assigning probability to the likelihood of an event occurring provides students with an opportunity to revisit and consolidate their work with fractions, decimal fractions, percentages and their equivalences.
Probability is a measure of the likelihood of an event occurring. Provide students with opportunities to describe and represent probabilities of an event happening from impossible (0% chance), which means this event will not happen under any circumstance, to fifty-fifty chance (50%), which means an event may or may not occur, to certain (100% chance), which means that an event will happen without a doubt. Use a probability scale marked with these percentages or a line continuum to ask students to position themselves to indicate the likelihood of an event happening.
Make explicit the ways probabilities can be written. For example, in a bag containing 5 blue marbles, 4 red marbles and 1 green marble, pulling a blue marble from a bag of 10, with replacement each time, is 510 , 12 , 0.5 or 50%. Representing problems visually enables students to list the possible outcomes.
Use different contexts to list possible outcomes, such as coin toss, dice rolls, spinners, bags containing different objects, or other events that have a random chance involved. For example, a spinner equally divided into six different coloured segments has a 1 in 6 chance of landing on one of those segments. Ask students to investigate the probabilities when there are larger segments of one colour. Discuss fairness and bias and the greater chance that the spinner has on landing on this larger segment.
Use questioning to prompt students to draw on their reasoning skills when discussing the likelihood of an event occurring in chance activities. Consider ways to enable students to grasp probability concepts and scaffold their learning. Student learning may be extended using equivalent fractions and by describing events to match the probabilities.
Teaching and learning summary:
- Use contexts where students describe the probability of an event occurring.
- Introduce a scale or continuum to describe the likelihood of an event occurring from zero to one.
- Make connections to prior learning about fractions, decimals and percentages.
- List the different possible outcomes of chance activities.
- Make explicit the language used to describe chance.
Students:
- represent probability on a probability scale from zero to one
- use the terms impossible, unlikely, equal chance, likely and certain
- express probabilities using fractions, decimals and percentages
- describe whether the probability of an event is random and/or fair
- explain their reasoning when discussing chance activities
- use manipulatives to model their solution and thinking.
Some students may:
- have difficulty explaining why an event is random and what the likely outcomes may be. Check for student understanding by investigating a die roll where one person wins if the number is odd while the other wins if the roll is an even number. Change the parameters so that they then use two dice, and one wins if the dice total 8 or more, while the other wins if it is 7 or under. Listen to them argue mathematically as to whether the game is random, fair or unfair.
- be able to express the probability of an event occurring using the language of chance but be unable to assign a value as a fraction, decimal or percentage. Use a number line and discuss fractions, decimal or percentages, starting with 50% as an equal chance, 0% as no chance and 100% as a certainty. Use enabling prompts to scaffold the learning.
- The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning about chance.
- We are using probability in real-life contexts.
Why are we learning about this?
- Probability is the chance or the likelihood of something happening. Understanding probability is important as it occurs in many areas of work and our daily lives.
What to do
Work out these problems. Give reasons for your answers to explain how you worked it out.
- If 30% of blood donors have ‘type A’ blood and you contact 100 people.
- What is the likelihood of finding a donor with ‘type A’ blood?
- Two How many people out of the 100 would you expect to have ‘type A’ blood?
- You need 150 donors with ‘type’ A blood. How many people would you expect to call to find 150 people with ‘type A’ blood?
- A lake contains two types of fish: brown trout and rainbow trout. The fish in the lake are 60% brown trout and 40% rainbow trout. Anglers catch the fish and release them back into the lake.
- Which fish are you more likely to catch?
- If you catch 10 fish, how many of each type are you likely to have?
- An angler catches 9 rainbow trout and 1 brown trout. Is this what you would expect? Explain your answer.
- A netballer has a great record of goal shooting. Nine times out of 10, the netballer scores a goal when they stand within 2 metres of the goals. Beyond 2 metres from the goal, they have an equal chance of missing or getting a goal.
- What is the likelihood they score a goal when standing 1 metre from the ring? Write this as a fraction, decimal and percentage.
- In a typical game, the netballer shoots at goal 50 times. How many goals would you expect to be scored if 30 of the shots are taken within 2 metres of the goal? Create a table or model to show your results.
Success criteria
I can:
- identify all possible outcomes of a chance experiment
- assign probabilities to a simple event.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Probability of an event
In this task, students describe the probability of an event using words and numbers.
Go to resource -

What's in the bag?
Students find out that with probabilistic situations there is no certain way to predict exactly what will happen.
Go to resource -
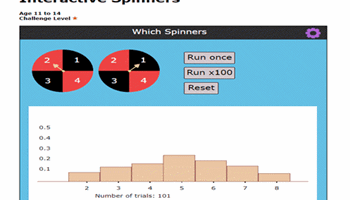
Interactive spinners
Use this task to discuss possible outcomes.
Go to resource -
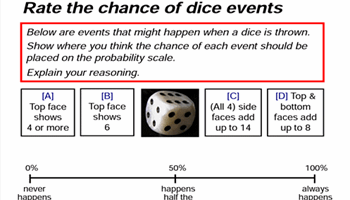
What do you know about probability?
Use this task to introduce students to the probability scale where they can place events based on probability values. Students can then explain their reasoning.
Go to resource -

reSolve: Probability
In this task, students calculate probabilities; represent probabilities as fractions, decimals and percentages; perform chance experiments with small and large sample sizes; and graph their results.
Go to resource -
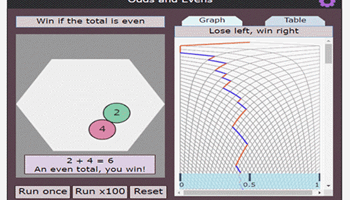
Odds and evens
This task requires students to use reasoning to list possible outcomes and decide whether the game is fair.
Go to resource -

Statistics and probability: chance Year 6 – teacher guide
Use this guide for background information on key concepts of probability.
Go to resource -

Coin shake-up
This problem solving activity has a statistics focus.
Go to resource
Assessment
By the end of Year 6, students are assigning probabilities using common fractions, decimal and percentages.
-
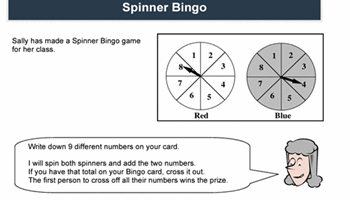
Spinner bingo
Students analyse a simple game and plan a winning strategy.
Go to resource -
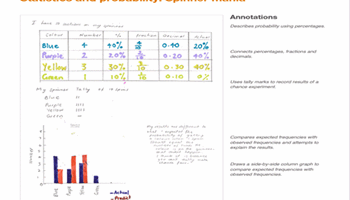
Mathematics Year 6 – ACARA
Refer to ACARA work sample 11, 'Statistics and probability: spinner mania'.
Go to resource -
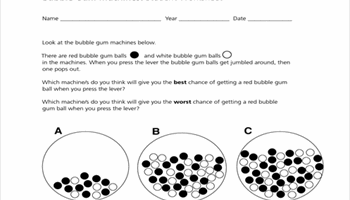
Bubblegum machines: student worksheet
Use this task to assess a student’s understanding of probability and ability to describe an event using the language of chance.
Go to resource -
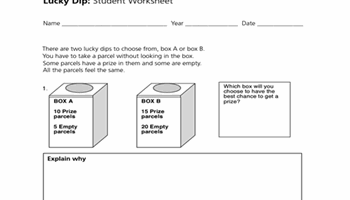
Lucky dip: student worksheet
Use this task to assess a student’s understanding of probability and ability to describe an event using the language of chance.
Go to resource