Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M5P01
Numeracy Progression: Understanding chance: progression: P3
At this level, students list the possible outcomes of chance experiments involving equally likely outcomes and compare them to those which are not equally likely.
As a class, use a probability scale (zero to one, impossible to certain), to discuss the chance of an event occurring. Suggest events where students must describe the outcomes of chance events as impossible, certain or somewhere in between.
Introduce relevant contexts involving chance that have equally likely outcomes to then discuss the possible outcomes. For example:
- a coin toss: heads, tails
- selecting a red card from a pack of 52 cards: 13 hearts and 13 diamonds
- rolling an even number on a die: 2, 4 or 6
- a spinner equally divided into four colours: red, blue, yellow, green.
Elicit from students that in these examples there is an equal chance for these events to occur, which is described as equally likely outcomes. Use the contexts to discuss fairness and use ‘what if’ scenarios to explore the idea of outcomes that are not equally likely, for example, the red segment on the spinner is changed to blue so there now are two blue segments. Refer to the probability scale, discuss as a class and indicate where these fit on the scale.
Use games for students to consider the probabilities of rolling two dice. Use these as a way of systematically listing all the possible outcomes and then discuss which totals are less/more likely to be rolled.
Raffles and lucky dips provide a useful context to discuss probabilities. As a class, discuss a raffle where students each put their name in a hat to be selected. The outcome includes each person’s name, so each person has the same chance of winning. Through questioning, prompt students to explain their reasoning when considering certain scenarios, for example, if a person has their name in the draw multiple times, or what would need to occur for a person to have a fifty-fifty chance of winning the raffle?
Teaching and learning summary:
- Investigate the probabilities of all outcomes for simple chance experiments.
- Make explicit chance experiments that involve equally likely outcomes and compare to those which are not equally likely.
- Discuss the element of fairness.

Students:
- use the language of chance
- order events on a probability scale from impossible to certain
- list possible outcomes of chance experiments
- describe what it means for outcomes to be equally likely and compare the number of possible and equally likely outcomes of chance events
- explain why some games are fair, and others are not.
Some students may:
- not realise that chance has no memory (for example, if a student has rolled four sixes in a row, they often believe the fifth roll cannot possibly be another six).
- be confused when comparing observed frequencies and expected frequencies, as they may not yet understand why observed frequencies might produce different results to expected frequencies. Conduct experiments where students must record the results, that is, their observations. They can then compare these to the expected results. Some examples:
- The probability of rolling a 6 on a die is 16 , so this would be the expected probability. This means if the die was rolled 600 times, it would be expected the number 6 would come up 100 times.
- Conduct an experiment where the student rolls the die 10 times and records the results for each roll (a frequency table could be used to record results). At the end of the experiment, students tally the number of times a 6 appeared. For example, the number 6 may have come up 2 times in the 10 rolls. As a fraction, this would be written as 210 which simplifies to 15 . In this case, the observed frequency does not match the expected frequency. Discuss why this is the case. Ask students to think about how to achieve an observed result that is closer to the expected result. What would happen if we rolled the dice another 10 times and then another 10 times again? Digital tools enable students to do this efficiently.
- incorrectly believe that similar to rolling one die where there is a 1 in 6 chance, rolling two dice would have a 1 in 12 chance of rolling a total. However, this is not the case. For example, rolling a total of 7 has a 6 out of 36 ( 16 ) chance, whereas rolling a total of 4 has only a 3 in 36 chance ( 112 ).
- confuse events with outcomes, for example, when rolling two dice and getting a total of 3 the outcome of [2,1] is different to [1,2] however the outcome is still a total of 3. There are two chances out of a possible of 36.
To address these, ask students to conduct repeated chance experiments, recording and interpreting the results.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to list the outcomes of a chance experiment.
Why are we learning about this?
- We are learning about probability and fairness.
What to do
- Play a game which usually uses dice, but instead of dice use your own spinning top.
- Make a spinning top that has an equal chance of an outcome happening. You will need a piece of card, felt markers and a pencil poked through the centre of the card to use an axis on which to spin.
- Record how you made your spinning top, and how you made sure there is an equal chance of an outcome happening.
Success criteria
I can:
- create a spinning top that has outcomes that are equally likely
- list the possible outcomes of my spinning top.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
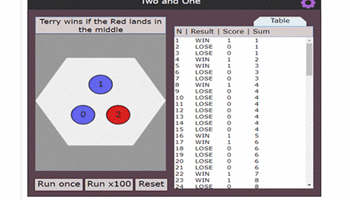
Two and one
This problem offers students the opportunity to investigate experimental probability and work systematically to find all possible outcomes and discuss fairness.
Go to resource -
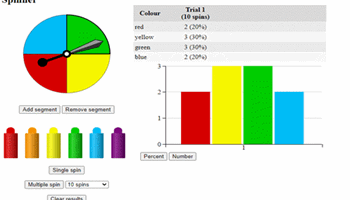
I’m spinning
In this task, students use spinners to develop an understanding of the probability of simple events occurring.
Go to resource -
Odds or sixes?
This problem gives learners the opportunity to describe and predict outcomes and consider the meaning of ‘fair’.
Go to resource -
The twelve-pointed star game
This game uses the rolling of two dice to explore possible outcomes.
Go to resource -

Luck of the draw
This activity provides an opportunity to integrate probability using the context of selling raffle tickets.
Go to resource -
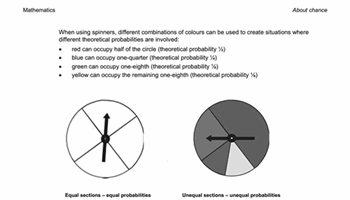
About chance
Use this resource for background knowledge about teaching chance and probability.
Go to resource -

Long running
In this unit we take samples of blocks from a bag and use them to make predictions about the blocks that the bag actually contains. We discuss the difference between theoretical probability and experimental estimates of probability.
Go to resource
Assessment
By the end of Year 5, students are conducting repeated chance experiments, listing the possible outcomes, estimating likelihoods, and making comparisons between those with and without equally likely outcomes.
-

Chance cards and student worksheets
Use this task to assess students’ understanding of probability and ability to describe an event using the language of chance.
Go to resource -

Mathematics – ACARA Year 5 annotated student work samples
Refer to ACARA work sample 11, 'Come in spinner' to assess students’ understanding of probability.
Go to resource