Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M4P01
Numeracy Progression: Understanding chance: progression: P3
At this level, students build on their language of chance and ability to order outcomes or events based on their likelihood of occurring. They begin working with independent and dependent events – independent events occur when one event does not affect the other, while dependent events are affected by previous events.
Use practical examples to allow students to discover the difference between dependent and independent events. Students may be familiar with independent events such as rolling a die, where there is a 1 in 6 chance of rolling a 6, or when tossing a coin and getting a ‘tail’ is a 1 out of 2 chance. In these examples, the probability of a second roll of the die or next toss of a coin is not dependent on the result of the first.
Contrast this with examples of how drawing a card from a pack of playing cards and not returning it to the pack changes the probability of future cards drawn. Another example is choosing coloured marbles from a bag. Make explicit that each time a coloured marble is selected and not replaced, the probabilities change.
Use the Concrete, Representational, Abstract (CRA) model to compare dependent and independent events, focusing on the probabilities of each event.
Teaching and learning summary:
- Describe possible everyday events and order by their chance of occurring.
- Use practical examples to investigate dependent and independent events.

Students:
- order events from impossible to certain, including ‘least likely’ to ‘most likely’ to occur
- explain the effect on probabilities when an item is not replaced in a chance experiment.
Some students may:
- be still developing their language skills and not fully understand the language of chance to then be able to relate these to the likelihood of an event occurring.
- tend to believe in luck (for example, they will have a better chance at rolling their favourite numbers).
- make predictions based on likes and interests (for example, their favourite colours for spinners).
- not realise that chance has no memory (for example, if a student has rolled four sixes in a row, they often believe the fifth roll cannot possibly be another six).
- not be yet able to understand the difference between independent and dependent events and not be able to explain the effect of replacement.
Teachers should use true/false statements to help uncover any student misconceptions as students discuss and respond to questions and examples. For example, statements can include:
- When rolling a die, the event of rolling a 6 is less likely than rolling a 3.
- If I toss 4 heads in a row, it is highly likely that the next will be tails.
- If there are 100 jellybeans in the bag with 50 green and 50 red, the event of selecting a green will always be a fifty-fifty chance even if the jellybeans are not replaced after each selection.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to describe possible everyday events and their chances of occurring.
- We are learning to use probability to solve a problem that draws on your understanding of probability.
Why are we learning about this?
- We use probability as a numerical measure of how likely an event is to happen.
What to do
Work out this problem, and record how you worked it out.
- Each box of cereal has a small prize, and there are five different prizes to collect. How many boxes of cereal would you expect to buy to get all of the different prizes?
- Can you think of a way to model this problem without buying any cereal?
Success criteria
I can:
- compare the likelihood of outcomes in a simple chance experiment
- conduct simple experiments with random generators
- make statements that acknowledge ‘randomness’ in a situation.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
A bit of a dicey problem
Students throw two regular, six-faced dice and discuss the chance of getting one particular result rather than any other.
Go to resource -
The twelve-pointed star game
This game offers a good context in which students can explore possible outcomes and think systematically about what scores are possible.
Go to resource -
Which when?
Students investigate probabilities using a spinner and then compare experimental results with expectations.
Go to resource -
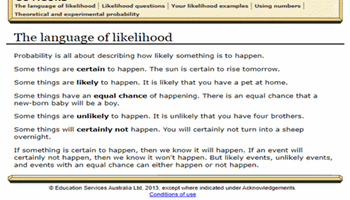
The foul food maker: go figure
Students explain how the use of simple words can describe the likelihood of everyday events.
Go to resource -
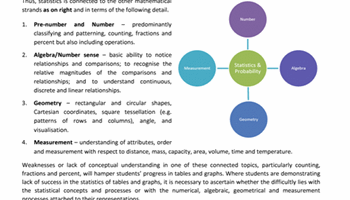
Statistics-and-probability: F-9
This resource provides background information and sample lessons.
Go to resource -

Dressing in the dark
This problem solving activity has a statistics focus
Go to resource
