Expected level of development
Australian Curriculum Mathematics V9: AC9M6N07, AC9M6N08
Numeracy Progression: Interpreting fractions: P7, Multiplicative strategies: P9, Understanding money: P8, Proportional thinking: P2
At this level, students use their knowledge of percentage and decimal equivalents to calculate percentage discounts. Example problem: a 30% discount on a $75 item can be found by converting 30% to its equivalent decimal fraction (0.3) and multiplying it by $75 to see that a 30% discount will be $22.50.
Encourage the development of a range of flexible strategies when solving problems related to finding the fraction, decimal fraction or percentage of quantity. To support this aim, ask students to find two or more ways to solve the problem. For example, a second way to solve the 30% discount on a $75 item would be to find 10% ($7.50) and multiply it by 3. This form of thinking, where students find the unit, can be used in the context of fractions – a students can find 56 of 30 kg by finding 16 (5 kg) and multiplying it by 5 (25 kg).
Use questioning to develop students’ ability to approximate numerical solutions. Questions like, ‘What is an estimate that is too high? What is an estimate that is too low?’ Ask the students to make sense of the problem, which ensures that they are doing more than applying computation methods without understanding. Look for opportunities to highlight and model efficient approximation strategies, for example,
52% is about 12 , 0.263 is about 14 .
Use dynamic software that uses region models (such as the GeoGebra percent visualisation tool) to help students link equivalent representations of fractions, decimal fractions and percentages.
Continue to model correct place value language when describing decimal fractions. Describe 12.8 as ‘twelve and eight tenths’ as opposed to ‘twelve point eight’ to help students understand its quantity and make connections to its fractional equivalent.
Teaching and learning summary:
- Make connections between fractions, decimal fractions and percentages.
- Model ways to use flexible strategies to calculate percentage discounts.
- Help students develop mental approximation strategies to encourage sense-making of quantities and operations involving fractions, decimal fractions and percentages.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to recognise equivalent fractions, decimal fractions and percentages.
Why are we learning about this?
- We can further our understanding of some of the different ways that rational numbers can be represented.
What to do
1. Write 45 as a decimal and percentage.
2. Use this hundredths grid to represent 45.
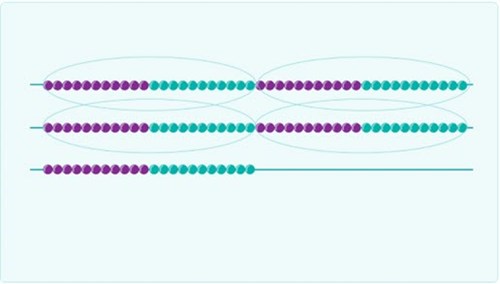
3. Use this bead string grid to represent 45.
4. Explain the connection between fractions, decimals and percentage using an example.
Success criteria
I can:
- interpret rational numbers shown as fractions, decimal fractions and percentages, and connect equivalent quantities.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Farm fence fractions
In this lesson, we explore fractions, decimals and perimeter.
Go to resource -
Fractional funds
Reinforce understanding of fractions in a practical context, by learning how to find a fraction or percentage of an amount, through budgeting.
Go to resource -
Let’s go shopping!
In this lesson, students calculate percentage discounts on a range of items offered through different pricing discounts and offers.
Go to resource -
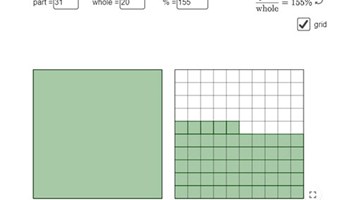
Percent visualisation
Use this resource to quickly and easily demonstrate the connection between fractions and percentage by showing different examples of parts of a whole.
Go to resource -
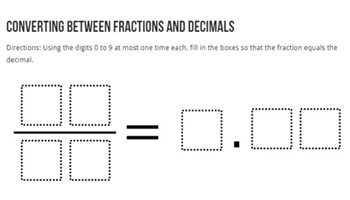
Converting between fractions and decimals
A fluency-building, open-ended task where students must use the digits 0 to 9, at most one time each, to fill in the boxes so that the fraction and the decimal are equivalent.
Go to resource -
Open middle: percentages
A fluency-building open-ended task where students must use the digits 0 to 9 at most one time each, to fill in the boxes to make a true equation involving percentages.
Go to resource -
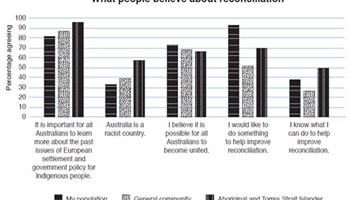
reSolve: Reconciliation data
This task interprets data of significance for Australian society and provides an opportunity to develop and use mathematical skills in a humanities and civics context.
Go to resource -
Operating with decimals
This learning sequence aims to develop student proficiency when adding, subtracting, multiplying and dividing with decimals.
Go to resource -
What’s for Lunch?
Students work collaboratively to reflect on the accuracy of their estimations, explaining and justifying their strategies, that include calculating basic discounts.
Go to resource
Assessment
By the end of Year 6, students order common fractions, giving reasons, and add and subtract fractions with related denominators.
-
Mathematics: Year 6: ACARA
Refer to work sample 4 'Number: Fractions, decimals, percentages and integers' for guidance on how to assess a student’s understanding of common fractions, decimals and percentages.
Go to resource -
Percentages as change (% can be more than 100)
This resource supports teachers to assess and find appropriate activities for students who need acceleration in their understanding and application of percentages as change.
Go to resource