Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M5N04
Numeracy Progression: Additive strategies: P9, Number and place value: P8
At this level, students recognise that fractions, decimal fractions and percentages are equivalent ways to represent and make sense of quantities. They learn about the different contexts where it makes sense to use one of the constructs to express a proportional relationship.
Once students understand fractions and decimal fractions, they can then explore equivalent representations of percentages. A useful way to conceptualise percentages is to think of them as fractions, where the amount is always described relative to 100. The term ‘per cent’ is another name for hundredths. For example, 75% is the same as 0.75 or 75100.
Provide opportunities for the students to sort, order and compare visual and symbolic representations of fractions, decimals and percentages. Emphasise number sense by asking students explain their thinking.
Use proportional concrete materials such as decimats or Cuisenaire rods to support conceptual understanding. Dynamic software using tangrams or pattern blocks can provide different contexts for students to explore proportional relationships. Stress the importance of equal-sized parts. For example, if a number line is partitioned into six equal-sized parts then the name and size of the part is sixths.
To support conceptual understanding, move beyond prototypical representations of rational numbers. One way to do this is to consider that while fractional parts must be the same size, they do not need to be the same shape.
Provide contexts for students to link improper fractions to percentages greater than 100%.
Use diagrammatic representations to help students recognise the fractions as a division construct. For example, students can think of 13 as 3 ÷ 5 which, when typed into a calculator will give a decimal solution. Dynamic software can be used to enable students to connect this thinking to visual models through partitioning 3 into 5 equal parts.
Teaching and learning summary:
- Demonstrate the link between fraction equivalence and percentages to describe, represent and compare relative size.
Students:
- make connections between concrete, visual and symbolic representations of fractions, decimal fractions and percentages
- explain why a chosen representation makes sense in specific contexts.
Some students may:
- have difficulties representing small percentages such as 1.2%, or percentages that include decimal fractions such as 40.5%. Area models such as decimats will help students understand and represent these quantities.
- think that the longer the decimal number the larger it is. For example, when comparing 0.3 and 0.258 they would consider the latter to be the larger because they revert to whole-number thinking and concentrate on the length of the numbers after the decimal. Other students may believe the opposite, that the shorter the decimal number the larger it is. For example, they may think 0.2 is larger than 0.25 as they think that a hundredth is smaller than a tenth.
- see 34 and 56 as equivalent as they are both one number away from being a whole number. Model residual thinking where students compare the size of the fraction that is needed to get to 1 (14 and 16 in the case above) to help them appreciate the size difference between the two fractions.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to represent decimals to three decimal places.
Why are we learning about this?
- Decimals are part of our everyday lives.
What to do
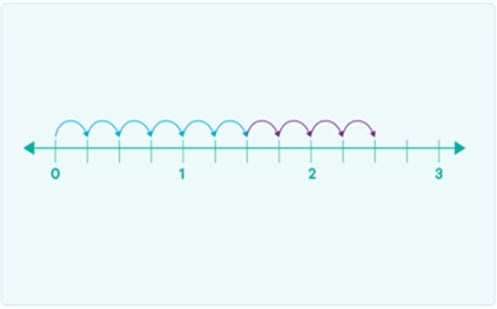
1. Have a think about the number 0.258.
Here is the number 0.258 shown on three different number lines.
- Can you see on the first number line 0.258 is in between 0.2 and 0.3?
- On the second number line the number 0.258 is shown between 0.25 and 0.26.
- On the third number line the position of 0.258 is shown on the number line.
2. Can you represent the number 0.625 on a number line? Draw your own number line to represent the number.
- Where might you see this number used? Give an example.
- How would you say the number 0.625? Write your answer down.
Success criteria
I can:
- partition a decimal number into its place value parts
- represent a decimal pictorially.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Map masterpiece
Students explore the world of house and garden design while delving into the fascinating realm of percentages.
Go to resource -

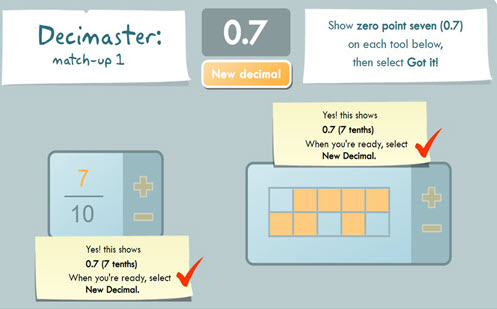
Decimaster: match-up 1
Using this interactive tool, students are presented with a decimal. They are required to determine the equivalent fraction and visual representation to match the given decimal.
Go to resource -
Beginning with percentages
This unit supports students to recognise percentages in everyday contexts, gain knowledge of simple percentages as proportions, and find simple percentages of amounts.
Go to resource -

Open middle: Related percentages
A fluency-building, open-ended task where students must use the digits 0 to 9 as many times as they want to create a correct number sentence using percentages and whole numbers.
Go to resource -
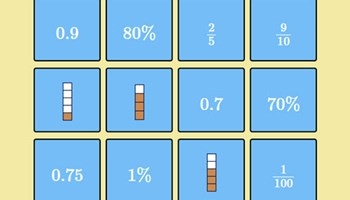
Matching fractions, decimals and percentages
Dynamic software where the aim of the game is to match pairs of cards. A good activity to reinforce equivalent representations and build fluency. There are five different levels of difficulty.
Go to resource -
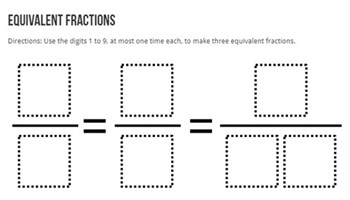
Open middle: Equivalent fractions
A fluency-building, open-ended task where students must use the digits 1 to 9, no more than one time each, to make three equivalent fractions.
Go to resource -

Doughnut percents
Students work collaboratively in teams to match equivalent representations of fractions, decimal fractions and percentages to form a doughnut shape.
Go to resource -

Quarter the cross: card sort
There are several mathematical investigation ideas in this resource. Card sort asks students to match visual and symbolic representations of 1/4.
Go to resource -

Keeping it in proportion
This learning sequence aims to develop student understanding of fractions and decimals.
Go to resource
