Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M6A01, AC9M6A03
Numeracy Progression: Number patterns and algebraic thinking: P5
At this level, students generate and investigate patterns using concrete materials, geometric shapes, calculators and spreadsheets. Some examples are growing patterns using dots, cubes or sticks; systematically exploring dividing by 9 or multiplying by 11 on a calculator or spreadsheet; and observing the differences between repeatedly adding or multiplying by the same number.
Students extend their work with patterns to create and use algorithms involving a sequence of steps and decisions that use rules to generate sets of numbers. They identify, interpret and explain emerging patterns.
Provide opportunities for students to learn how to design algorithms for standard mathematical procedures they already know. They will use informal language to describe to a computer (robot) what to do to perform the operation. To do this, they will need to break down the operation into small steps, look for decision points and use repetitions. It may help students to use concrete materials to practise the operation being performed. Guide students to break down the problem into simple steps and yes/no decisions. Also include instructions on how to go back to a previous step.
A function machine can be used to explore rules. Demonstrate how a function machine works by adding a value and observing the output. Make a table showing input and output for students to recognise the pattern more easily. Provide opportunity for students to use function machines to model the input-output process of machines that generate tables of values for simple rules such as: ‘The output is 3 times the input subtract 2.’ They use function machines in reverse to determine which input leads to a given output.
Teaching and learning summary:
- Investigate patterns using concrete materials such as toothpicks to create a growing pattern of triangles. Use 3 toothpicks for one triangle, 5 for 2 triangles, 7 for 3 triangles. Describe the pattern as: ‘Multiply the number of triangles by 2 and then add one for the extra toothpick in the first triangle.’
- Use a calculator or spreadsheet to generate patterns such as 1 ÷ 9, 2 ÷ 9, 3 ÷ 9, or 100 ÷ 99, 101 ÷ 99, 102 ÷ 99, identifying patterns, including similarities and differences.
- Design and use an algorithm that involves a sequence of steps to generate a number sequence. Adapt the algorithm and describe and explain differences observed, for example, ‘double and add 1’ compared to ‘add 1 first and then double’.
- Use function machines to generate outputs based on a rule/algorithm. Describe and explain relationships and any emerging patterns.
Students:
- create and investigate patterns using concrete materials and digital tools such as calculators and spreadsheets, and identify any emerging patterns, including similarities and differences
- design and use an algorithm that involves a sequence of steps to generate a number sequence and describe and explain relationships observed
- use a function machine to produce a table of values
- describe patterns produced by a function machine.
Some students may:
- go into ‘auto-pilot’, simply adding all the numbers and ignoring the given context.
- have difficulty with the notion of variable and the ideas of ‘input’ and ‘output’ for a rule.
- have difficulty moving from an everyday language description of a process to a sequence of instructions or a template for a function machine.
- assign literal meanings to letters (variables), for example, 3a interpreted as 3 apples, rather than understanding that variables can be thought of as objects or ‘placeholders’ in a rule.
- have limited understanding of the properties of numbers and operations (for example, multiplication only understood in terms of groups of; division not seen as the inverse of multiplication).
To address these, provide multiple opportunities to use concrete materials to explore patterns and write rules for growing and shrinking patterns. Use function machines to develop algorithmic thinking.
Refer to the resource Common misunderstandings: Level 6 – Generalising. This was developed from a large body of research that examined the various difficulties students experience with algebraic thinking.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention: using a function machine
- We are learning to use a function machine to represent a sequence of instructions and fill in a table of values.
- We are learning to recognise and describe any emerging pattern that results from the use of a function machine.
Why are we learning about this?
- It is important in many practical situations to have a clear set of instructions for carrying out a process, such as a recipe for preparing a meal, putting together a piece of furniture, or calculating using a formula. Function machines provide a way of describing an input-output process using a simple diagram.
What to do
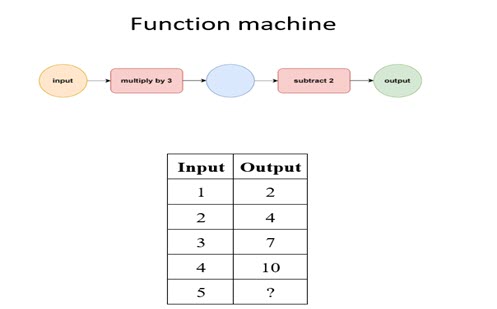
The following diagram shows a function machine that calculates output values for given input values.

1. Describe in words what the function machine does to the input value.
2. Complete the diagram below to show what the output value is for an input value of 4.

3. Use the function machine and a calculator to complete the table of values below:
| Input | Output |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
4. Describe any pattern you observe in the output values from the table.
5. Find the input value which gives an output value of 67 and explain how you obtained the answer.
6. Below is a blank diagram of a function machine.
a. Use the diagram to construct a function machine that halves a number then adds one.
b. Use the machine above and a calculator, to complete the following table of values and describe any pattern you observe in the output values from the table.
| Input | Output |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
c. Find the input value which gives an output value of 11.5 and explain how you obtained the answer.
Success criteria
I can:
- use a function machine to create outputs from inputs and complete a table of values
- describe an emerging pattern from a table of values created using a function machine.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

The truth about triangles and squares
Students find a rule to describe any member of a number sequence and express it in words.
Go to resource -

Hunting for patterns and rules
This learning sequence encourages students to develop their understanding of patterns and algebra. Pattern recognition supports the development of computational thinking.
Go to resource -

Consecutive numbers
Students work together sharing results and making decisions about which consecutive numbers to look at next.
Go to resource -
Music to my ears
This activity centres on factors and multiples in a very practical context, and introduces the idea of common multiples.
Go to resource -

Up and down staircases
This engaging, practical problem gives learners the opportunity to explore patterns, explain patterns and generalise.
Go to resource -

Picturing square numbers
This problem develops the links between visualisation, verbal description and algebraic representation.
Go to resource -

An algorithm to perform the order of operations
Use this task to introduce algorithms using the order of operations. Students write a series of steps and questions for a robot to follow.
Go to resource -

Algebra basics: Video and teaching guide
Use this video as a springboard to introduce algebraic thinking, and to apply that thinking to a financial context, drawing on reasoning.
Go to resource -

Table mats
Students use a table to find a rule for a geometric pattern and writing the rule for the relationship.
Go to resource -

Building patterns
Students represent the relationships between pattern number and number of tiles using tables, graphs and rules, in order to predict further terms of the pattern.
Go to resource