Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M10SP01
Numeracy Progression: n/a
At this level, students are familiar with the basics of geometry and have been introduced to proof when looking at similar triangles. They will be extending and applying these skills and using deductive reasoning and geometric theorems to solve spatial problems in relation to congruency and angle relationships.
Show students how to apply this knowledge and use the correct geometrical vocabulary when describing the effect on plane shapes that have undergone transformations. Students use their analysis skills to interpret the spatial concepts of a particular problem and demonstrate how to construct a logical and reasoned proof, clearly explaining justifications and reasons when presenting conclusions. Critical thinking is an important life skill to nourish.
Use dynamic geometry software to aid students’ analysis and approach to problem-solving. Visually correlating change and noting congruence of congruent triangle and angle properties, for instance, scaffolds reasoning.
Having a firm understanding of these concepts will support students going on to study mathematics, including topics such as circle geometry.
Teaching and learning summary:
- Revise students’ knowledge of geometry.
- Revise students’ knowledge of the terms ‘similarity’ and ‘congruence’.
- Introduce the concept of mathematical proof: the language and symbols.
- Demonstrate the conditions for two triangles to be congruent or similar.
- Show how to construct a logical geometric proof.
- Describe deductive reasoning and how you can apply it in geometrical problems; give examples.
- Demonstrate how theorems can help solve spatial problems.
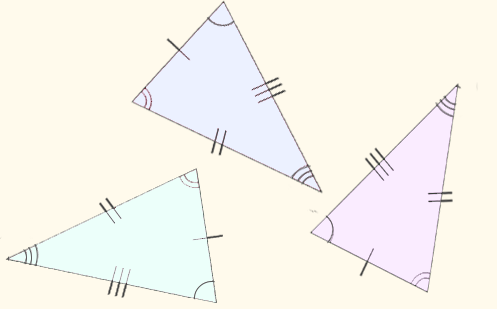
Students:
- recognise and prove that two triangles are congruent
- know the conditions for two triangles to be congruent
- know the conditions for two triangles to be similar
- use knowledge of angles and plane shapes to prove two shapes are congruent or similar
- solve problems using knowledge of congruence and similarity
- construct a logical geometric proof
- begin to use deductive reasoning to proofs involving plane shapes
- use geometric theorems to solve spatial problems.
There are many misconceptions and misunderstandings about mathematical proof. It is a difficult concept for students. AAMT Top Drawer offers a number of articles and activities that address these.
It is difficult for students to grasp logical arguments and make connections with a series of logical progressions of thought. Students may confuse the difference between deductive and inductive reasoning. Explain that inductive reasoning begins with a particular scenario and makes generalisations about a conclusion; that is, you make inducements to arrive at a conclusion. The problem with this is the conclusion may be incorrect.
Deductive reasoning requires more evidence presented in a logical progression that naturally leads to a conclusion, so that the conclusion is true without the possibility of being incorrect. Asking students to use reasoning is difficult to apply, so begin with easy problems with known geometric knowledge and gradually increase the difficulty of the problems.
Students also make errors when they are constructing proofs. For example, students:
- assume the conclusion in order to prove the conclusion
- are unsure on how to start the proof
- provide unnecessary examples to supplement their valid proofs
- misunderstand definitions
- do not use enough explanations in their steps of reasoning
- use incorrect steps.
Explain that every line of argument needs to be true and not just a claim. Explain that the layout of the proof needs to be able to be followed in a neat and logical manner. Encourage students to use reasoning phrases and vocabulary, for example, 'Statement B follows Statement A because …'.
Give feedback and encourage fellow students to give feedback on clarity of statements.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how to write a formal proof of a geometric property using the correct mathematic language and notation.
- We are learning how to apply geometrical properties to solve geometry problems.
Why are we learning about this?
- There are many areas where knowledge of shape and angle are useful.
- It is important that you can communicate your ideas using the correct mathematical terminology and notation.
- If you are going on to study mathematics at a higher level, a knowledge of formal proof is important.
What to do
Proving congruence with support
- Open this webpage, Proving triangles congruent
- Work through the three sections:
- SSS: Dynamic Proof!
- SAS: Dynamic Proof!
- ASA Theorem?
In each section you can view videos and do short exercises to build and test your understanding.
Success criteria
- I can use knowledge of angles and plane shapes to prove two shapes are congruent or similar.
- construct a logical geometric proof.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
reSolve: Mechanical linkages – Geometry proofs
This inquiry is part of a series and is designed to build on students’ previous geometrical knowledge, enabling them to develop their own proofs.
Go to resource -
Rigid motion, congruent triangles and proof
This resource consists of a series of annotated lessons on how to introduce the concepts of proof and congruence.
Go to resource -
Congruence
This resource consists of a series of virtual manipulatives that demonstrate various geometrical properties in a dynamic setting.
Go to resource -
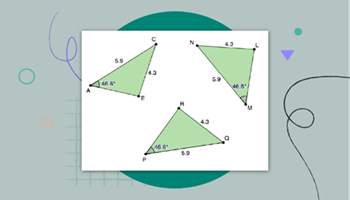
IM Geometry: congruence
In this unit, students begin by reasoning about the relationships between congruent parts of figures and congruent figures. They use transformations as tools for reasoning and generalising.
Go to resource -
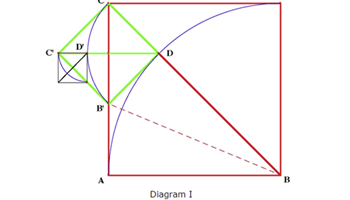
Proof
A series of articles on the history and different types of proof.
Go to resource -

Types of mathematical proof
An article on the different types of mathematical proof.
Go to resource
Assessment
By the end of Year 10, students can use deductive reasoning and theorems to solve spatial problems.
-
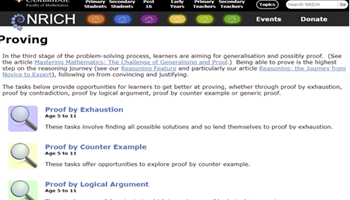
Practise proving
An opportunity for students to practise proving, whether by exhaustion, contradiction, logical argument, counter example or generic proof.
Go to resource -
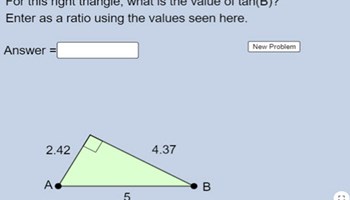
Identifying trig ratios
This activity presents a series of right-angled triangles and asks students to enter a specific ratio.
Go to resource