Year level: 4

Strand: Number

Lesson length: 60 mins

In this lesson, students will use mathematical modelling to make decisions based on the purchasing of gifts. Students will explore different ways to estimate and form possible options for purchasing, ensuring they do not go over budget.

Buying presents Image

Achievement standard

Students use mathematical modelling to solve financial and other practical problems, formulating the problem using number sentences, solving the problem, choosing efficient strategies and interpreting results in terms of the situation.

Content descriptions

Students use mathematical modelling to solve practical problems involving additive and multiplicative situations including financial contexts; formulate the problems using number sentences and choose efficient calculation strategies, using digital tools where appropriate; interpret and communicate solutions in terms of the situation. AC9M4N08

General capabilities

Numeracy:

Critical and Creative Thinking:

  • Analysing (Interpret concepts and problems)
  • Inquiring (Identify, Process and Evaluate information)
  • Observe the working out in students' workbooks while they are developing a plan or solving the problem and make notes on what you observe.
  • Listen to students' discussions with each other regarding their strategy choices.
  • Notice the level of difficulty based on the student’s choice of strategy. Did students change their strategy after the summarise stage? Did they select a more efficient strategy?
  • Use estimation approaches to make an estimate.
  • Estimate approximate money values of multiples of items.
  • Follow steps for problem-solving and know problem-solving strategies they could use to find solutions.
  • Calculate multiple money amounts.
  • Use relevant strategies to calculate the difference between money values involving dollars and cents.
  • Adopt a growth mindset and persist with a problem they do not have an immediate solution for.

Some students may:

  • find moving from additive to multiplicative thinking when calculating costs of the same item purchased multiple times (repeated addition to multiplication)
  • find shifting to abstract thinking difficult – estimation is an approximate value, not an exact value
  • need to move from inefficient to efficient strategies that are embedded in their learning
  • have challenges reading and understanding the problem – there is choice in the way the money can be distributed, and students must decide to purchase items based on their value and how much money they have in total (the problem doesn’t state that the amount spent on each person is of equal value or that the amount that remains unspent).

What you need:

Leaning goals

Learning intention

We are using mathematical modelling to solve problems involving money (budget).

Success criteria

By the end of this lesson, students can:

  • estimate the cost of multiple items
  • use the 4 steps to problem-solving
  • explore different ways to spend a given value on items with whole-dollar amounts
  • show different ways to find the total of money values
  • find the difference between money values
  • use efficient strategies when solving money problems.

Why are we learning about this?

From an early age, students learn that if we need to buy something we need money. In many cultures students receive gifts from family members during special occasions, for example, birthdays.

As students grow older they experience purchasing items and working within a budget themselves. They learn that working with money is an essential life skill. They will also need to make financial decisions based on their earnings and what they can afford.

Learning hook 5 mins

Discuss family groupings and family members. The task in this lesson revolves around an uncle buying presents for his nieces and nephews.

Ensure students are familiar with these relationships so they can engage in the learning activity.

Ask:

Who has an aunty or uncle? How are you related to them?

Which other family members do you have? What is your relationship to them?

Explore 35 mins

Explain to the students that today we will using mathematical modelling to solve a maths problem related to purchasing gifts. We will:

  • make decisions based on the purchasing of gifts
  • infer the types of toys a 10–12 year old would like from a selection of 4 gifts
  • explore different ways to estimate and make decisions on possible gifts to purchase, ensuring we do not go over budget.

To help us, we will follow a 4-step method to guide our work and thinking.

  • Share the 4-step problem-solving process. Introduce each of the steps to the students over the course of the lesson.

        Slide 2

Image showing 4 steps to problem solving: identify/describe, plan, communicate and apply/do.

 

  • Present the problem to the students.
  • Support the students to read and understand the problem. Unpack any unfamiliar vocabulary. Encourage students to identify and describe the problem mathematically. Ask the students to follow this process:
  • Read the problem.
  • Read the problem again (one part at a time) identifying key words/numbers/symbols. Make pictures of the story in your mind.
  • Say what is happening in the story to a friend.
  • What do we know? What do we need to find out?

Buying presents

Wally wants to buy a present for each of his nieces and nephews. He has two nieces and three nephews. They are all between 10 and 12 years old.

Wally has a budget of $600.

He has narrowed the possible presents down to four items.

Four possible gifts with different prices: Scooter $96 Family board game $65 Basketball $89 Building blocks set $109

  1. Record your ideas about how Uncle Wally could spend the money to buy the presents.
  2. Show how you might use rounding to estimate:
    • how many multiples of each item and you could buy for $600
    • how many different items you could buy for $600.
  3. Show some ways Wally could spend the money to buy presents for his nieces and nephews.
    • Model the different ways Wally could spend the money.
    • Use a plan to organise your thoughts and select problem-solving strategies that are appropriate for the task.
    • Show the steps you used and all your working out.
  4. Is there any money left over? If so, how much? Show your working out.

Teacher note: This scenario can be adapted to an aunt or grandparent. When choosing gifts, we carefully considered gender equity. You can choose different gifts for the lesson, with adjustments to the worksheet and presentation. Some students may assign a particular type of gift to a particular gender. This could be an opportunity to discuss gender stereotypes with the class. Challenge these stereotypes rather than ignore them. 

Differentiation

Enabling prompt: Open-ended question

Extending prompt: How did you decide which gift Wally would purchase for each relative? What would you suggest Wally does with any left-over money?

Summary and reflection 15 mins

  • Ask students:

What are some of the strategies you selected to help solve this problem?

Why did you decide on these strategies?

How are these strategies connected to the problem?

  • Encourage the students you identified earlier to share their strategies with their peers.

Support students in their explanation with mathematical vocabulary and sequence of steps. As students are sharing their thinking, record their strategy using materials/pictures and numbers (words) on an anchor chart.

  • Acknowledge the student’s work using their initials and reflect on the strategies shared.

Examples of strategies

Select strategy/ies from the examples below to share with the students (depending on students’ learning needs).

Begin to model the selected strategy/ies.

Estimate

Image for scooter with tag Scooter $96 each.

  • Round the cost of a scooter to the nearest multiple of 10 or 100. 96 is closer to 100 with a difference of 4.

Image showing rounding $96 to $90 or $100.

Round $96 to $100

5 children @ $100 = $500

$600 – $500 = $100

If Wally was to buy each of his nieces and nephews a scooter, he would have 5 scooters and $100 left.

  • The most expensive item is the building blocks.

Image showing children's blocks with a tag Building blocks kit: $109 each.

Round $109 to the nearest multiple of 10 that is greater than $109. The nearest multiple is $110.

5 children x $110 = $550

$600 - $550 = $50

  • The basketball and board game each cost less than the scooter, therefore Wally will have enough money to purchase one of these items each for his nieces and nephews.

Partitioning (Multiplication):

If Wally was to purchase the same item for each niece/nephew, he could use multiplication to find the total cost. To support you with this process we can partition the tens and ones. For example:

Purchase a scooter for each niece/nephew (5 scooters).

5 x $96

Diagram showing how we can partition the tens and ones for 5 x$90 = $450.

Model: we could also apply the same strategy if we were to purchase two different types of gifts. In this case we would use partitioning to find the cost of the two different items purchased and then add the totals together.

Partitioning (Division):

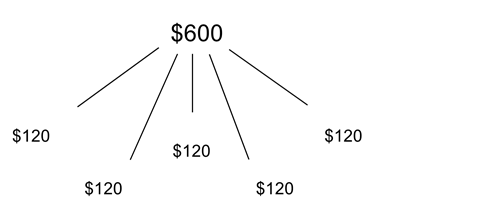
We can work out how much money Wally has to spend on each niece/nephew if he was to share the amount equally between them all.

Share $600 equally between 5 nieces/nephews.

Partition $600 into 5 equal parts.

There is an allocation of $120 each.

Diagram showing how we can use partitioning to share $600 into 5 parts ($120 each).

Doubling:

If Wally was to purchase the same item for each niece/nephew, he could use the doubling strategy for multiplication. For example:

  • one Family Board Game for each niece/nephew or 5 x $65
  • Double = x 2
  • Double/double = x 4

We can use the double/double strategy to find the cost of 4 family game boards then add the cost of the 5th board.

  • Double $65 = $130
  • Double $130 = $260
  • Double/double $65 = $260
  • $260 + $65 (5th scooter) = $325

We could also use the double strategy when purchasing different items, for example, 3 family game boards and 2 basketballs.

  • 3 x $65 = double $65 + $65 = $195
  • 2 x $89 = double $89 = $178
  • $195 + $178 = $373

If students have difficulty with doubling $89 you could model how to use partitioning to support this process. For example:

  • double $80 + double $9 = ?
  • $160 + $18 = $178.

Difference:

To calculate the difference the amount spent and the total amount we can use different strategies. In this example we show how to use an open number line.

  • Total cost of 5 scooters = 5 x $96 = $480
  • Difference between $480 and $600 is $120

Open number line showing a jump from $480 to $500 ($20) and then from $500 to $600 ($100) = $120.