Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M9SP02
Numeracy Progression: Understanding geometric properties: P7, Proportional thinking: P7
At this level, students can apply the enlargement transformation to shapes by hand and with dynamic geometry software. They will identify aspects of the shape that remain the same after enlargement, and those that change and justify this with appropriate explanations.
The important aspects to consider are a shape’s dimensions, area, and volume. It is critical to define what is meant mathematically by ‘enlargement’ and ‘similarity’.
Explore different pairs of shapes to determine whether they have been enlarged with similarity or slight deformity. It is beneficial to present some pairs with one shape rotated or reflected position. This tests students to think critically. Some students may jump to the conclusion that the shapes are no longer similar – a useful teachable moment.
Afford opportunities to find relationships between the side lengths and the magnitude of the angles. Ask questions: can all the new side lengths be divided by the same number to return to the original dimensions (dilation). This highlights the first aspects of change and continuity and that although the lengths of the sides are changed by the transformation, the ratios between the sides remain unchanged. If this is not the case, the two shapes are not similar.
Give opportunities for students to explore the area of shapes, and the surface area and volume of 3D shapes. Question students on the pattern of continuation that is observed in the increase in size of the side lengths for all these cases. Dynamic software applications are particularly useful here and can visually demonstrate that area of a 2D shape and the surface area of its corresponding solid is increased by multiplying by the square of the scale factor, and that the volume of the solid is increased by multiplying by the cube of the scale factor. Use questioning again to clarify the distinction between the rules for area, surface area and volume. Why does surface area (for solids) follow the same rule as area (plane shapes)?
This topic is the gateway into trigonometrical ratios – AC9M9SP01
Teaching and learning summary:
- Revise congruence and similarity of plane shapes and the associated rules.
- Revise ratio in the context of scale drawing.
- Use examples of enlargement to help explain the meaning of scale factor.
- Test for similarity first before making any other conclusions.
- Look for patterns in the changes to the area and volume of enlarged shapes.
- Draw connections between these patterns and the meaning of similarity, and dimensionality.
- Use the properties of similarity to solve problems.
- Use dynamic geometry software to perform enlargements and calculate areas and volumes.
- Use reasoning to explain similarities and differences between pairs or sets of similar shapes or objects.
Students:
- check whether shapes are similar and use this as the basis for drawing additional conclusions
- use dynamic geometry software to enlarge shapes and objects
- know the relationship and patterns between side lengths, area and volume, the scale factor, and similarity.
- can explain why the side lengths, area, and volume change according to the patterns observed.
- can explain why the ratio between sides, magnitude of angles, and form, are the only unchanged aspects.
- solve problems relating to similarity and enlargement.
Some students may:
- confuse similarity and congruence.
- not check the scale factor is the same for every side.
- assume a diagram is to scale and make assumptions based on this assumption.
- not realise that the orientation of an object does not affect its properties.
- believe that corresponding sides are ‘matching’ regardless of the orientation of the shape.
- assume that area and volume increase by the same factor as the side lengths.
- assume that surface area and area are impacted differently by enlargement.
Stimulate curiosity and allow for students to discover patterns to explore a range of enlargements. A convenient way to clarify this to students is through digital applications like PowerPoint. Demonstrate how a shape can be enlarged by dragging one of its corners to become larger; show that by holding the shift key during enlargement the shape maintains uniformity or it risks distortion. Students learn that similarity is defined by all sides increasing by the same scale factor, and the angles remaining constant.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how to test whether an enlarged shape has maintained its form.
- We are learning how to apply patterns and draw conclusions about similar enlarged shapes.
Why are we learning about this?
Using one piece of information to infer more complex information is an important skill. Area and volume can be time-consuming to compute as we need to know several measurements and then perform a series of calculations. If we can draw conclusions about these based on a shape’s similarity to one another, we can save ourselves a lot of time and tedious calculation. And don’t discount how smart you’ll feel when you can reel off a series of facts about a shape without taking a single measurement! All thanks to the power of patterns.
What to do
Our homes are filled with screens these days. Televisions, phones, tablets, smart home hubs, laptops, gaming devices, and PCs. Which is your favourite viewing experience? Is there any mathematical similarity between these different screens?
Let’s investigate any patterns that exist between the variety of screens around the home.
Below is a table with a list of devices that you might find at home.
| Device | Length | Width | Ratio |
| Living room TV | |||
| Video game console | |||
| Smart phone | |||
| Laptop |
- Create your own table to record the dimensions of a variety of screens in your home.
- Add an additional column for recording the screen ratio. This is calculated by dividing the length by the width.
- You may notice the ratio 16 : 9 is frequently used to refer to 'widescreen'. This ratio means that the length is approximately 1.78 times the width.
- Do any of your devices match this common ratio?
- Are any of your screens similar? That is only true if they have the same ratio!
- If any of your screens are similar you should determine the scale factor between them. This is done by finding the number that you can multiply the dimensions of the smaller screen by to produce the dimensions of the larger screen.
How much larger is the area of the larger screen? (Remember – area increases by the square of the scale factor.) - Consider your favourite screen. Which is the most pleasurable to view?
- How could you adjust the dimensions of the other screens to make them similar to your favourite?
- List a set of new dimensions for the other screens that would most closely match their original size, while taking on the ratio of your favourite.
Success criteria
- I can test objects around my home for similarity and apply the patterns of enlargement to them.
- I can test whether an enlarged shape has maintained its form.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
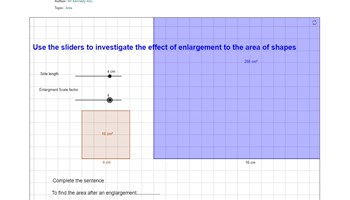
Enlargement and area
This investigation uses dynamic geometry to investigate the connection between scale factor and area, with examples and questions.
Go to resource -

Scale factor inquiry
This investigation looks at the relationship between enlargement, surface area and volume.
Go to resource -
Congruence
This resource consists of a series of virtual manipulatives that demonstrate various geometrical properties in a dynamic setting.
Go to resource -
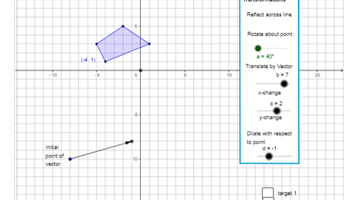
Applet for multiple transformations
This interactive allows for multiple practise opportunities to experiment with different transformations. Students choose a target and try to map the original to it.
Go to resource
Assessment
By the end of Year 9, students can apply the enlargement transformation to images of shapes and objects, and interpret results.
-
Mathematics: work sample portfolio
Refer to the Work sample 4: Similar triangles, which gives an example of a geometric investigation on triangle congruence. Other areas work samples, provide practise with trigonometry and Pythagoras.
Go to resource -
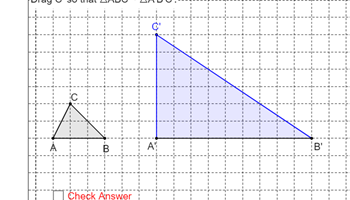
Similar figures
This resource is an interactive assessment opportunity for students to test whether shapes have been transformed or are similar.
Go to resource