Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8A04
Numeracy Progression: Number patterns and algebraic thinking: P7
At this level, students bring together knowledge and skills on linear functions and relations, and experiment with digital tools to investigate systematic variation of parameters to show the effect. Students cement their understanding of the 'm' and the 'c' in the traditional linear function y = mx + c by observing visual transformations.
The benefit of using digital tools is that results are immediate and easy to manipulate, allowing practice for many trials. Working in this way, students can make conjectures, test and notice change, and identify emerging patterns. Students should aim to immediately visualise any linear function by considering where it crosses the y-axis, whether it slopes up or down, and how steeply.
For example, students may vary integers: what happens to the gradient/slope for y = x, y = 2x, y = x2, y = 3x, y = x3 and y = –x. Students should also vary the value of c for y = mx + c equations, and observe the graph being transformed in both the positive and negative y-directions.
Teaching and learning summary:
- Use digital tools so that students can manipulate related functions to make conjectures, and test and identify emerging patterns between equations and their functions.
- Encourage a systematic approach when manipulating parameters so students may identify the meaning behind pronumerals and constants.
Students will:
- vary the parameters of graphs of related functions
- use digital tools for easy repetition and manipulation
- make conjectures, test and identify emerging patterns and trends
- visualise linear functions
- restrict intervals.
Students may:
- be uncomfortable with plotting linear equations and identifying emerging patterns.
- be able to operate digital tools easily but fail to make connections and find patterns both graphically and algebraically.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how to adjust the values of a linear function to create any straight line we want.
- We are learning how restricting the values for or adjusts the length of the straight line.
Why are we learning about this?
Visualisation is key to solving complex problems. Mathematical equations are merely symbolic representations of lines, curves, shapes or solids. Far more information is contained in the image than in the equation itself. Developing the ability to intuit what an equation’s graph looks like makes it much easier to solve related problems and make sense of solutions.
What to do
Write your name in linear graphs!
Using the GeoGebra calculator, we will create a series of graphs that join to write our initials or name, or to draw a picture. The more you practise and the better you understand the role of each value in a linear function, the more complex your output can be.
Let’s quickly review the basics and consider: y = mx + c
m controls the slope of the line. If it is a positive number, the line will slope up. If it is a negative number, the line will slope down. Remember, we always think in terms of left-to-right. As m increases in size, the steepness of the line increases too.
c controls the point at which the line crosses the y-axis. Whatever value c takes is the point at which it intercepts the y-axis. Therefore, increasing or decreasing this value will move the graph up or down.
Write my name
To write my initials I need to create an S and a G. I will begin with the S as an example to get you started. To challenge myself I’ve decided to make a funky slanted S. It is made up of three straight line graphs.
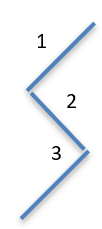
- First I will make Line 1 (green line below, f), and then I’ll use this as the basis for the other two lines. Line 2 (blue line, g) is perpendicular to Line 1. Hint: when the gradients (m) of perpendicular lines are multiplied together, the result is always –1. So, if I made the gradient of Line 1 equal to 3, I’ll need to set the gradient of Line 2 to –1 3.
- I need to shift Line 2 down, which I will do by adjusting the c value until it is in the exact spot I want.
- Line 3 (purple line, h) should have an identical gradient to Line 1, but it will also need to be shifted down.
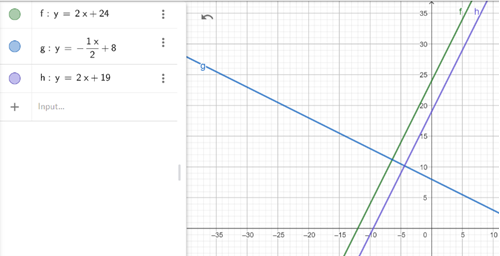
You can see Line 1 and Line 3 are parallel and perpendicular to Line 2 in the example above. But it is difficult to see the S! There’s one last step.
The lines currently go off to infinity in both directions. They need to be shortened. I will do this by restricting the values in each function. I’ll need to know where the lines intersect first. GeoGebra can help with that. Simply click on the point of intersection.
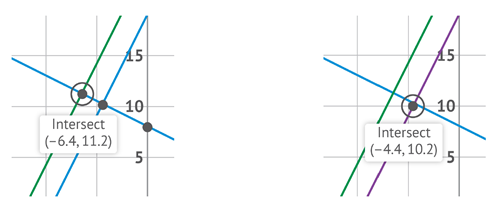
I need to restrict the x values of Line 2 to between x=–6.4 and x=–4.4 only. The x-values of Line 1 can begin at x=–6.4, and the x-values of Line 3 (h) must stop at x=–4.4 I’ll play around with the other end points until I am happy with the look of my S.
To restrict the x-values in GeoGebra we need to use a ‘function’. Type function into the input space and select the second option. You will need to type in the name of the line you want to restrict, the x value you want it to begin at, and the x value you want it to end at.
E.g. Function(g,–6.4,–4.4)
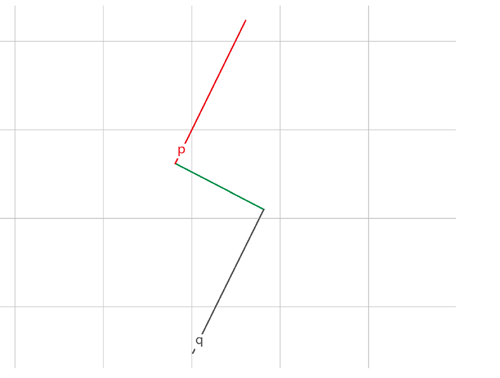
Lastly, uncheck the original graph of ‘g’ so you can only see the restricted version. Now I can move on to the G in my initials.
Start with your initials, then try your first name and finally attempt to draw something.
Success criteria
- I can adjust the m and c values in a linear function to create my desired straight line.
- I can restrict the domain of a function to select only the piece of the line required.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
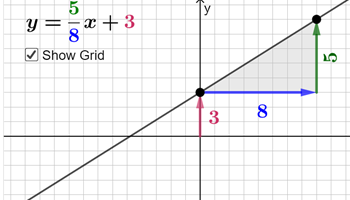
Linear equation anatomy
Students can vary parameters to explore these various digital interactives to understand the algebraic language and its graphical complement.
Go to resource -
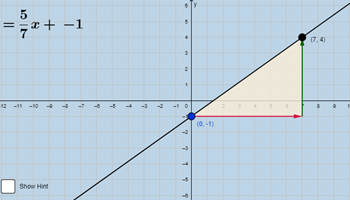
Blueprint equation of a line
Similar to ‘Linear equation anatomy’, students can vary parameters to test the outcome. However, for this activity, students use a downloadable worksheet to work backwards starting from (x, y) coordinates on the Cartesian plane. This investigation could be used as homework task or test.
Go to resource -

How far does it move?
The teacher notes for this interactive activity allow students to visually explore the notion of movement over time and how this can be expressed as a distance/time graph. Students can make conjectures and test the interactive to find the solution or best approach to the problem.
Go to resource -

Fill me up
Challenge students with this task on graphical representations of a real-world problem – a constant stream of water filling different types of flasks. Ask students to identify when (in time) lines of their graph are straight and when they are not. Can they identify and understand why or why not this is the case in relation to the shape of containers?
Go to resource
Assessment
By the end of Year 8, students can make and test conjectures involving linear relations using digital tools and make generalising emerging patterns.
-

Fill me up
Challenge students with this task on graphical representations of a real-world problem – a constant stream of water filling different types of flasks. Ask students to identify when (in time) lines of their graph are straight and when they are not. Can they identify and understand why or why not this is the case in relation to the shape of containers?
Go to resource -

Blueprint equation of a line
Similar to ‘Linear equation anatomy’, students can vary parameters to test the outcome. However, for this activity, students use a downloadable worksheet to work backwards starting from (x, y) coordinates on the Cartesian plane. This investigation could be used as homework task or test.
Go to resource -
Linear models
This interactive assessment task walks students through linear relationships and functions using real-world data.
Go to resource