Planning tool

Students:

• understand the differences between categorical and numerical (discrete and continuous) data
• calculate the range, mean, median and mode by hand and with the aid of a calculator or spreadsheet software
• describe the usefulness of measures of central tendency and spread
• determine the most appropriate measure of central tendency for a skewed distribution
• make reasonable predictions about the mean and median from a given data display.

Some students may:

• be disorganised in how they collect data.
• find it difficult to use the terms 'mean', 'median' and 'mode' instead of 'average', 'middle' and 'most frequent'.
• grasp the distinction between discrete and continuous.
• find data analysis and interpretation abstract in comparison.
• regularly mistake positive and negative skew.
• want to make inferences beyond the scope of the data.
• infuse personal biases into their analysis.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.

Learning intention

• We are systematically collecting data about fuel consumption over an extended period.
• We can accurately measure the centre and spread of the data.
• We can recognise patterns in the data that may inform decision-making.

Why are we learning about this?

Everything we do generates data, and this data is valuable. Using statistics to analyse data, we can answer almost any question we can think of. We need to be careful to gather the right data, measure it accurately and make sensible interpretations. In this activity we will collect, measure and visualise data about our vehicle fuel consumption.

What to do

1. Monitor your family’s (or a friend’s family’s) car fuel consumption with statistical rigour for at least a week. You’ll need to be patient, as good data analysis takes time. To spot patterns and trends, we need enough data. Maybe you have a big road trip coming up – that could be the perfect opportunity to try out this activity.

• Begin data collection the day the tank is filled and keep going until it’s empty. Measuring litres consumed each day would require special equipment, so instead record the total volume of fuel in the tank, then monitor the kilometres travelled each day.
• Set up some routines to ensure you get an accurate measurement each day. Let the car user know what you are doing, so they can remind you too. At the end of each day, you will need to read the car’s odometer.
• Challenge: if you have access to several vehicles, try to keep track of them all, using multiple copies of the table. Comparison is one of the most useful forms of statistical analysis.
• Labelling data: try to label your data as discrete or continuous. This may depend on the display output shown in the car.

2. Collect and record data in a table like the one below.  

3. Display the data using spreadsheet software, such as Excel, or create a graph or chart by hand.

• If using a spreadsheet, enter your values and find the tool that analyses the data for you and creates a graph or chart. In Excel, you would use the Data Analysis tool. Here is an example.

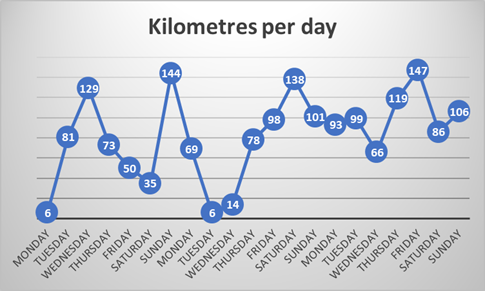
• Why do you think I chose a line graph to display this data?
• What design choices could I have made to improve the readability and usefulness of this graph?

4. Before doing any calculations, we can sometimes spot patterns in the data that begin to ‘tell a story’. This data has been collected randomly and there is no discernible pattern. Your data will be collected, therefore it is not random data. 

5. Calculate the measures of central tendency (mean, median and mode) and measure of spread (range) for your data. You can use spreadsheet technology to help you.

• How spread is your data?
• Do the kilometres travelled fluctuate heavily, or is it consistent?
• Does anything from your notes explain why?
• Did you have many ‘average’ days in which your kilometres travelled was like the mean? Why might this be?
• What recommendations would you make to your family or friend based on the data?
• Is your usage above or below Australian averages? The Australian Bureau of Statistics has plenty of data you can consult.

Success criteria

• I can carefully collect and accurately measure real-world data.
• I can recognise patterns in my data and consider whether they are significant.
• I can make recommendations based on statistical analysis.