Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M7N04
Numeracy Progression: Additive strategies: P9, Interpreting fractions: P8, Number and place value: P10
At this level, students extend their understanding of equivalence of fraction with visual representations (such as a number line that extends beyond zero), concrete materials, common multiples and fraction walls. Students learn to work with equivalence and explore when fractions are not equivalent and what this means.
Students learn to express one quantity as a fraction of another. This requires students to be able to identify which of the given numbers represent the whole and is therefore the denominator. Students simplify or cancel down fractions, when applicable. They should be shown how to use digital technology, such as a calculator, to efficiently simplify fractions when appropriate.
Students are introduced to percentages as fractions of one hundred. The connections between fractions, decimals and percentages should be demonstrated. Show students how these are represented and how they can be converted from one form to another. The use of concrete materials and visual aids will help understanding.
Students dive deeper and are required to explain equivalences in various forms: percentages, decimals, fractions and simplified fractions. Students explore positive, negative and mixed fractions, how they are represented and where they sit on a real number line. Knowing how they sit around zero will help consolidate the continuum of numbers and form the basis for future mathematical work.
Teaching and learning summary:
- Extend students’ knowledge of fractions to negative, positive and mixed fractions.
- Revise and extend students’ understanding of equivalence.
- Use visual aids, fraction walls, number lines and diagrams to show equivalence.
- Revise the terms ‘denominator’ and ‘numerator’ and relate and apply these to problems involving finding fractions of a quantity.
- Introduce percentage as ‘out of one hundred’.
- Demonstrate the connections between fractions, percentages and decimals.
- Demonstrate how to convert from one number type to another.
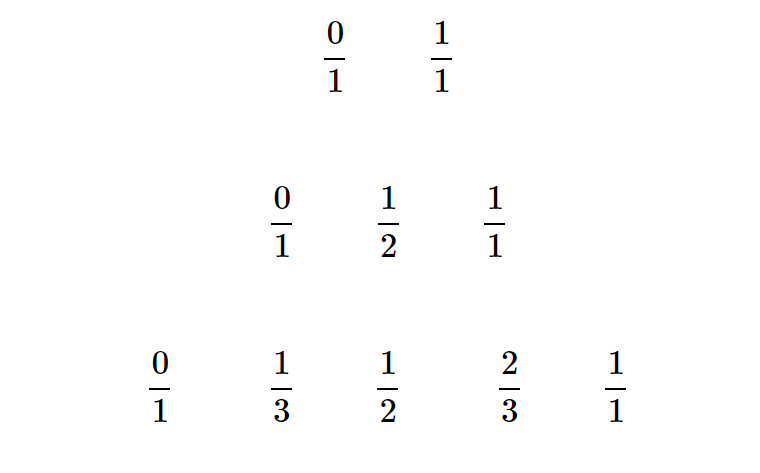
Students:
- extend their knowledge of fractions to negative fractions
- calculate equivalent fractions from any starting denominator
- understand the terms ‘denominator’ and ‘numerator’
- express one quantity as a fraction of another
- express a fraction in simplest form using common divisors
- know that percentage means ‘out of one hundred’
- understand that fractions, decimals and percentages are three ways to represent numbers
- convert from one number type to another
- represent positive and negative fractions and mixed numerals on various intervals on a number line.
Some students may:
- confuse the numerator and denominator.
- believe that the larger denominator is the larger fraction when making comparisons.
- not realise that fractions, decimals and percentages are three ways of expressing the same value.
- find converting decimal percentage into a decimal difficult.
- believe a decimal can be written as a fraction using the same digits. For example, students write 2.9 as 29 .
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
We are learning to compare fractions, decimals and percentages by plotting them on a number line.
Why are we learning about this?
If you know about decimals, fractions and percentages, then you can solve many practical problems in your everyday life. For instance, imagine not being able to understand what your ATAR score means, or what the interest on your car loan amounts to for your monthly repayments. Imagine starting your career in hairdressing but being unable to mix colours because you do not understand the idea of proportions. Maths is useful. Trust us!
What to do
How many sausage rolls can I make?
Warning: this activity could make you hungry.

Everyone enjoys a sausage roll for lunch or at a party! Let’s work out how many sausage rolls we can make from one packet of pastry.
A packet of pastry contains 10 sheets. We can make one really long sausage roll per sheet and then slice them to make two or three large sausage rolls, or we could make five or six cuts to make party-size sausage rolls.
Let’s think about this.
To make large sausage rolls, we could halve our long piece, or we could cut it into thirds. In this case, I have created a table to work out the total number of large sausage rolls that could be made relative to the number of cuts made. Record these in a table like the one below.
| Number of cuts | Fraction | Number of sausage rolls per sheet | Total number of sausage rolls |
| None | 1 | 1 massive sausage roll | 10 |
| 1 | 1 2 | 2 | 20 |
| 2 | 1 3 | 3 | 30 |
To make the party-size sausage rolls, we will need to cut our long piece into fourths, fifths, sixths or even sevenths.
- How many party-sized sausage rolls can I make if I have 10 sheets of pastry?
- Record these in a table like the one below.
| Number of cuts | Fraction | Number of sausage rolls per sheet | Total number of sausage rolls |
| 3 | 1 4 | 4 | 40 |
| 4 | 1 5 | 5 | 50 |
| 5 | 1 6 | 6 | 60 |
| 6 | 1 7 | 7 | 70 |
Don’t cut yet!
Before slicing (that’s if you’re really making them, of course), let’s make sure the sausage rolls are approximately equal in length. We can practise where we would make our cuts using a number line and figure out how many divisions we would make per sheet. Then we could work out how many we would have altogether.
- Below is a line to practise. You can draw one out yourself on a piece of paper.
- Put an X where you want your cuts to be.
- Above the X, write the fraction you were thinking of, say 1 2 or 1 3 .
- Here’s an example. Do this for all sorts of fractions and see how many sausage rolls you can make with one packet of pastry. Remember: one packet contains 10 sheets of pastry.
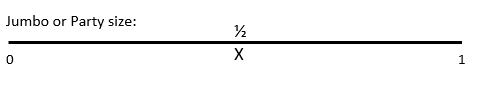
How many people are coming?
Now, let’s do some backward thinking.
Say we decide to make 100 party-sized sausage rolls because we think that will be plenty for our party of friends coming over. (Of course, we can eat the leftovers later.) If we have ten sheets and we divide each sheet so that we have ten rolls per sheet, we will make 100. We know this because 10 × 10 = 100.
Once we know how many sausage rolls we have altogether, we can play with different proportions to see how many sausage rolls each person could have depending on how many friends turn up.
Consider where on the number line below you would mark 1 2 , 1 3 , 1 4 , 1 5 and 1 8 .
This line is a little different to the one above as it represents the total number of sausage rolls (100) on the bottom right-hand side.

- How many sausage rolls would be equal to 1 2 of all the sausage rolls?
-
Mark with an X where half would be, then write the number of sausage rolls that amounts to directly below the line. Did you get 50? That means, if only one other person shows up including me, we would have 50 sausage rolls each!
- Your turn. What if there are four people altogether. Mark Xs on the line and figure out how many each person receives by writing the number directly below them.
- What about five people?
- What if there are nine people altogether?
- How do you think caterers estimate how much food to make when they supply party-food for parties?
Success criteria
- I can identify and explain the equivalence between a fraction, decimal and percentage.
- I can represent fractions and decimals on a number line.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Mathletes in motion
In this lesson, students use mathematical modelling to explain equivalence between fractions, decimals and percentages.
Go to resource -

Patterns, rules and graphs
In this lesson, students use games to learn about space and location on a Cartesian plane.
Go to resource -

Practical numbers: Part 2
In this lesson we use the context of an ancient bazaar to investigate measurement systems.
Go to resource -
Fractions on a number line
This sequence of interactive lessons and activities visually demonstrates where fractions exist on a number line.
Go to resource -
Equivalence fractions
Use this interactive in class to demonstrate equivalent fractions for students to make a visual connection to numbers.
Go to resource -
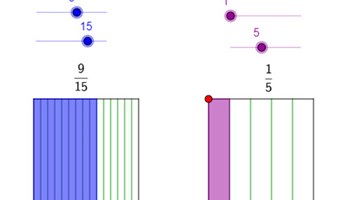
Simplifying fractions
This interactive can be used to show how a fraction may be visualised when simplifying fractions using greatest common factors.
Go to resource -
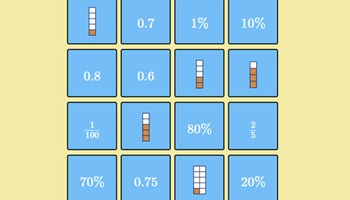
Matching fractions, decimals and percentages
Match the fractions to their equivalent decimals or percentages and progress through the levels. How far can you go!?
Go to resource
Assessment
By the end of Year 7, students find equivalent representations of rational numbers and represent rational numbers on a number line.
-

Fraction of a quantity
This set of worked examples demonstrates various strategies for identifying the fraction of a given quantity. The worked examples are followed by a series of similar questions for students to practise.
Go to resource -

Farey sequences
This investigation challenges students to think about comparing fractions and finding patterns.
Go to resource -
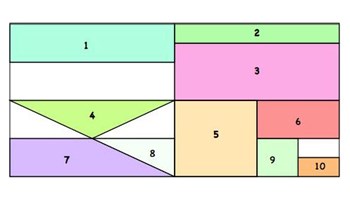
Rectangle tangle
This investigation combines students’ knowledge of fractions and area. Students must calculate the fraction of the total area each part represents.
Go to resource