Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8N01, AC9M8N03
Numeracy Progression: n/a
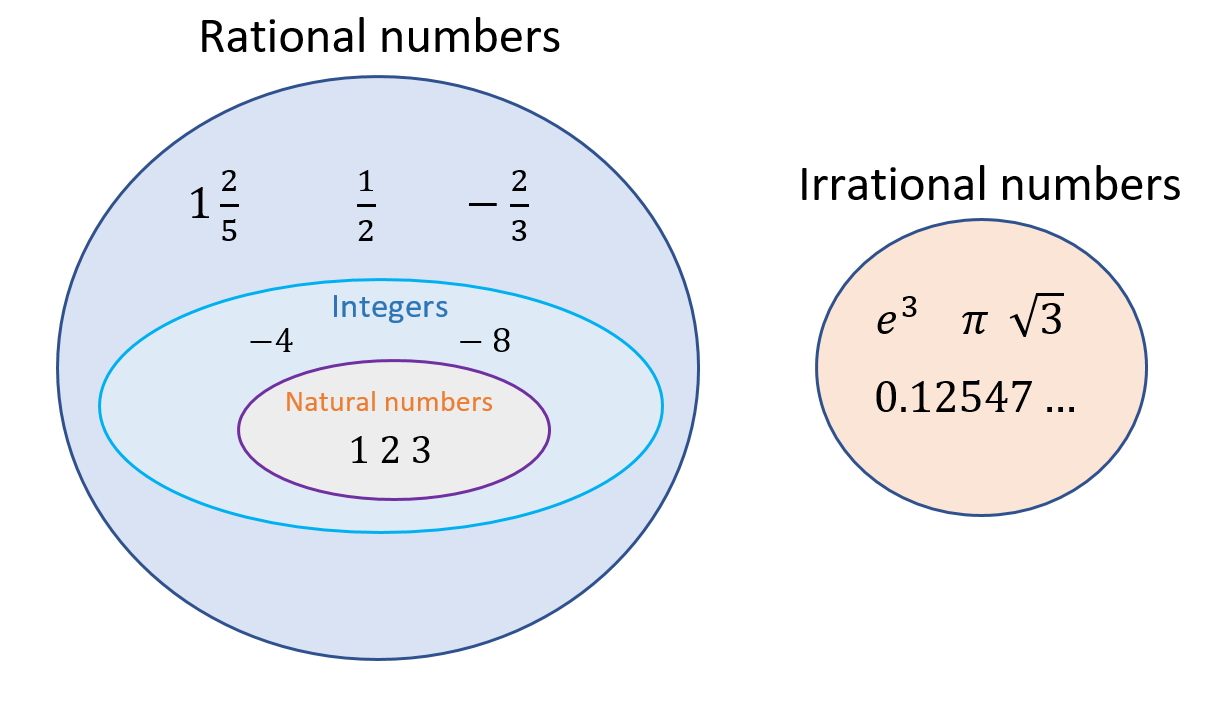
Students are introduced to ‘real’ numbers and ‘irrational’ numbers. Take time to explain the real number system so that students understand that irrational numbers are part of the real number group. Infographics, such as the diagram to the right, help students think about how numbers are grouped and connected with each other. Talk about the properties of each so that students know how to handle them with calculations. The most common irrational numbers are π (pi) and √2. When calculating with these, we often use approximations and rounding. Make connections by asking students to find these values on a real number line and use real-world contexts. Draw right-angle triangles to illustrate the natural existence of square roots.
Connect student knowledge on ratios and pi to find the circumference and diameter of any circle to the irrational value of pi using circular objects and other concrete materials. Set up an activity in which students create a wheel and roll it along a flat surface, marking the start and end points of a full revolution and comparing the distance between the two points to the wheel's diameter. Draw historical connections to Archimedes who may have first observed pi by watching the wheels of carriages in the market.
Introduce students to the concept of decimals that recur, by looking for repeating patterns, and decimals that terminate. Use fractions to demonstrate this with denominators. Contrast this to the random nature of pi's decimals. Discuss how patterns still occur in this randomness, such as six 9s in succession starting at position 762 (called Feynman Point). Students can be 'pi hunters' and search for interesting points in pi or try to find their date of birth. There are several online tools to support this activity.
Use digital programs and calculators to experiment with many variations, as well as representations. The aim is for students to recognise, identify, compare and choose the appropriate representations for instances of recurring decimals. Ensure students use ‘dot notation’ or bar notation to represent a recurring decimal. Students can use short division to convert fractions into decimals and identify patterns. What is the maximum number of random numbers before it must repeat? Why is this the case? What is the connection to remainders?
Teaching and learning summary:
- Introduce students to the real number system.
- Discuss the meaning of irrational numbers.
- Use digital tools to explore contexts or situations that use irrational numbers.
- Classify decimals as terminating for non-terminating and use appropriate notation to represent them.
- Look for repeating patterns in non-terminating decimals.
Students:
- know what is meant by an irrational number and recognise them in other contexts
- understand that when operating with an irrational number, we often use approximations and exact values, identifying the situations in which each would be preferable
- recognise if a decimal is terminating or not
- express a recurring decimal using the correct notation
- use digital tools when working with irrational numbers.
Some students may:
- not understand that the repeating pattern in a decimal can have many digits. Explore fractions with 7 as the denominator to demonstrate this.
- not have a good understanding of the real number system and cannot determine if a number is rational or irrational.
- not appreciate that using an approximation such as 3.14 for pi is an estimation. Encourage students to feel comfortable to leave solutions in terms of pi.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to recognise terminating, recurring and non-terminating decimals.
- We will express a fraction as a recurring decimal or a terminating decimal.
- We are learning to understand irrational numbers, including pi.
Why are we learning about this?
Decimals are used widely in our lives and building an awareness of the decimal system is important. Our money is based on a decimal system, and the price of petrol and the amount of gas are examples that are expressed using decimals.
What's not as obvious is how widespread irrational numbers are in our lives too. Many of the most important numbers in mathematics are irrational, and they pop up everywhere.
What to do
Step into the shoes of some of history's most famous mathematicians and discover just how common irrational numbers are.
Activity 1
- Find any piece of A-sized paper. A4, A3 or even A0 – it makes no difference in this activity. I wonder if you can figure out why!
- Measure the two dimensions of the sheet, then use a calculator to divide the length by the width.
- Type the number you found into a search engine. What's so special about it?
Activity 2
- Now take two of the most basic numbers in mathematics: 0 and 1.
- Add them together and write the result as the next number in a list. I think it’s safe to say you now have 0, 1, 1.
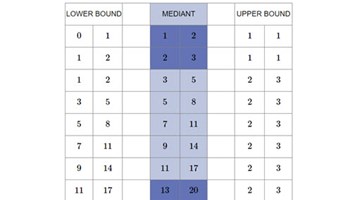
- Repeat this process multiple times and then transfer your sequence into a table like the one below.
- To calculate the ratio, you need to divide the new number by the previous one in the sequence.
- What do you notice about the ratio? Do you recognise this sequence?
| Number | Ratio |
| 0 | – |
| 1 | 0 ÷ 1 = 0 |
| 1 | 1 ÷ 1 = 1 |
| 2 | 1 ÷ 2 = 0.5 |
| 3 | ... |
See what more you can learn about this incredible sequence online. You have now discovered the most irrational number that exists. Don’t believe me? See if you can find out why that’s true and explain it to a friend. You’ll be blown away.
Here are two additional activities to help develop your skills.
Activity 3: Terminating and recurring decimals
Complete the interactive questions and check your answers.
Year 8 Investigating terminating and recurring decimals (amsi.org.au)
Activity 4: Irrational numbers including pi
Complete the interactive questions and check your answers.
Year 8 Investigating irrational numbers including pi (amsi.org.au)
Success criteria
- I can convert fractions into recurring decimals.
- I can present a fraction as a terminating decimal.
- I can place irrational numbers on a number line.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Pythagoras investigations and applications
In this lesson students work in small groups to investigate the application of Pythagoras’ theorem to problems in a practical or theoretical context.
Go to resource -

Pythagorean triples
In this lesson students undertake a mathematical exploration to find Pythagorean triples.
Go to resource -
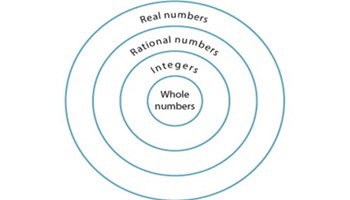
Investigating irrational numbers including pi
This interactive resource provides teachers and students with a detailed explanation of irrational numbers including pi with accompanying examples.
Go to resource -

Real numbers
This teacher guide on the real number system provides examples of classroom activities and teacher question stems. The activities are based on the BitL tool.
Go to resource -
An introduction to irrational numbers
This teacher resource gives explanation and guidance on irrational numbers including recurring decimals and the square root of two. There are games involving irrational numbers.
Go to resource -
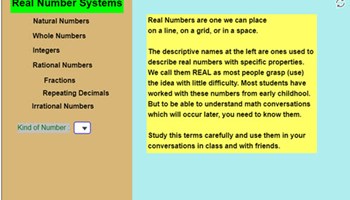
Real number classification
This interactive flow chart allows students to step down through the levels of categorisation of numbers click by click. Students use the sliders to reveal the next group with examples.
Go to resource -
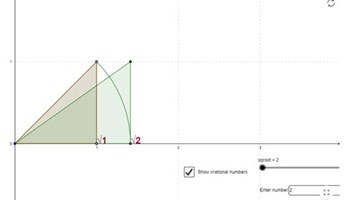
Irrational numbers on a number line
This interactive activity could be presented in class to show where irrational numbers sit on the number line.
Go to resource -
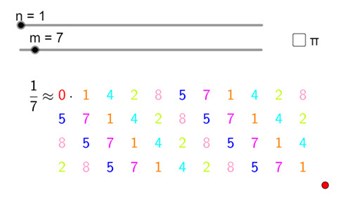
Patterns in decimals
This interactive allows students to experiment with the denominator and numerator to explore trends found in decimal representation.
Go to resource -

Putting Life on Mars
Students develop fluency by using knowledge about place value to make sense of very large and very small numbers.
Go to resource -

How old is the (Pythagorean) theorem?
In this lesson students learn about Pythagoras’ theorem and its application in calculating lengths in right-angled triangles.
Go to resource -

Pythagoras: Cartesian coordinate plane
In this lesson students calculate the distance between any two points on the Cartesian coordinate plane using Pythagoras’ theorem.
Go to resource
Assessment
By the end of Year 8, students can recognise irrational numbers, including square roots and pi, in various contexts. Students can use digital tools to investigate terminating and recurring decimals.
-
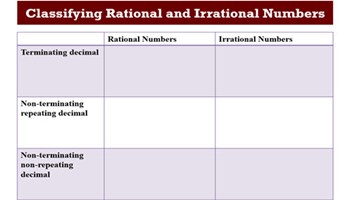
Classifying rational and irrational numbers
This unit is intended to help you assess how well students can distinguish between rational and irrational numbers and identify students having difficulties with this topic area.
Go to resource -
Square roots on a number line
Use this formative assessment to have students investigate irrational numbers, circles and triangles, and make estimations, such as area or length, in real-world scenarios.
Go to resource -

MYMC Level 8: Proficiency Rubrics
A formative assessment rubric template for the Level 8 Middle Years Maths Challenges that teachers can modify and tailor to each challenge and proficiency.
Go to resource