Expected level of development
Australian Curriculum Mathematics V9: AC9M7M04 and AC9M7M05
Numeracy Progression: Understanding geometric properties: P6
At this level, students identify corresponding, alternate and co-interior angles on parallel lines crossed by a transversal (a line that intersects two or more parallel lines). They apply this learning to geometrically prove that interior angles of a triangle sum to 180, and then extrapolate to all convex polygons.
It is important for students to construct parallel lines using a protractor and ruler, providing an opportunity for them to understand what it means for lines to ‘point in the same direction’. Students should know that parallel lines never intersect. This is where the concept of a transversal can be introduced, with students discovering that the angles formed at each line will always be identical. It is crucial students see that this concept is the nature of parallel lines. Ask questions so that they can explain ‘why’, using their new knowledge.
Constructing perpendicular lines with compasses is an excellent independent activity for students. ‘Who can figure out a method to construct two perfectly perpendicular lines without a protractor?’ For context and engagement, students could first learn how Ancient Greeks made mathematical discoveries using only a compass and straight-edge, without the measuring tools we have today. The activity can conclude by cementing the fact that perpendicular angles always intersect at a right angle.
Introduce students to formal geometric proof, investigating the interior angle sum of a triangle, with a focus on the reasons why it is true. Discuss what is important as justification. Connect the interior angle proof for triangles to other polygons. With concrete materials students can construct a range of polygons using only triangles and record the number of triangles it takes to construct polygons with varying numbers of sides. Conclude the reasoning by stating the angle sum formula for all convex polygons.
Diagrams are vital to help students recognise corresponding, alternate, and co-interior angles. Presenting examples of parallel lines drawn at different orientations ensures students can recognise these angles in a range of contexts. To support understanding, it is recommended that students learn via hands-on activities such as measuring angles or using dynamic geometry software.
Highlight the value of logical and consistent labelling when constructing or working with diagrams involving angles and lines to help solve or model problems. Practise naming angles and segments from labelled diagrams as well as labelling diagrams themselves. Using the correct symbols and notation should be regarded as essential to correctly solving problems.
Teaching and learning summary:
- Identify and classify angles as corresponding, alternate or co-interior on parallel lines crossed by a transversal.
- Construct parallel and perpendicular lines using their properties, compasses, protractors, and a ruler, or geometry software.
- Connect and build on students’ prior knowledge of angles and related areas.
- Develop students’ vocabulary of terms relating to angles and geometry.
- Label and interpret diagrams involving lines and angles and use mathematical notation to name different elements.
- Challenge students to use their vocabulary and notation when solving problems or providing justification for a solution.
- Recognise the conditions for lines to be parallel and perpendicular.
- Demonstrate how to construct angles, parallel lines and perpendicular lines.
- Prove the interior angle sum for triangles using parallel lines and alternate angles. Expand this theorem to polygons in general.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I can identify and determine the purpose of parallel and perpendicular lines in our physical world.
- I can prove the interior angle sum for a triangle.
- I will understand and use the correct vocabulary and notation associated with geometry.
Why are we learning about this?
No matter where you look you are bound to find parallel and perpendicular lines. We use their properties to make our buildings strong and sport fields fair. Understanding these properties, and the angles they form, means we can harness their power too.
What to do
Task 1
Grab your camera and free up some storage, we’ve got lots of photos to take!
- Find as many examples of parallel and perpendicular lines as you can around your home, garden, or neighbourhood.
- Snap a photo of each.
- Once you’re happy with the album you’ve put together, find a pen and paper, or your laptop.
- For each photo try and explain why the parallel or perpendicular lines are present there, and what value they provide. For example, why is your phone screen framed by two sets of parallel lines, one set perpendicular to the other? Yes, you’re right, they make a rectangle. But why is that a good choice for a phone screen? Why not have slanted sides?
Task 2
Challenge!
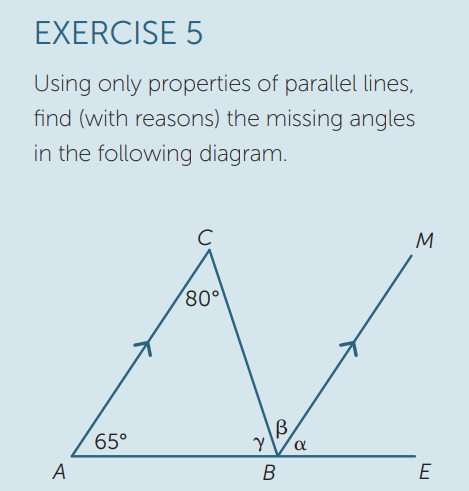
- By adding only a single line to this diagram that creates a pair of parallel lines, can you prove that all angles in a triangle must add up to 180°.
- To achieve this, you will need to carefully label the angles so you can refer to them in your reasoning.
- Ask yourself, does the proof I’ve provided have adequate reasons to justify it?
Hint: can you connect a set of angles that form a straight angle with the angles inside the triangle?
Success criteria
- I can identify parallel and perpendicular.
- I recognise the conditions for lines to be parallel and perpendicular and describe why they are valuable in our world.
- I understand and use the correct vocabulary and notation associated with geometry.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -
Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Angles and parallel lines
In this lesson, students will engage in various activities to explore angles between parallel lines in a navigational context.
Go to resource -
Parallel lines and angle sum of a triangle
This resource focuses on drawing representations of solid objects and gives detailed explanations of the curriculum content, with worked examples and assessment questions.
Go to resource -
Introduction to plane geometry
This module is for teachers who wish to consolidate their content knowledge on the topic of two-dimensional geometry.
Go to resource -
Alternate interior angles
First of a series of lessons that explore angles and parallel lines using dynamic geometry.
Go to resource -
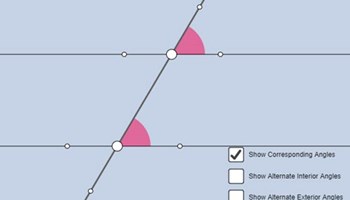
Parallel lines & related angles
This resource contains multiple activities that demonstrate the properties of angles and parallel lines together with assessment.
Go to resource
Assessment
By the end of Year 7, students can apply knowledge of angle relationships and the sum of angles in a triangle to solve problems and apply this to other shapes and the size of unknown angles. Students can explain their thinking and reasons.
-
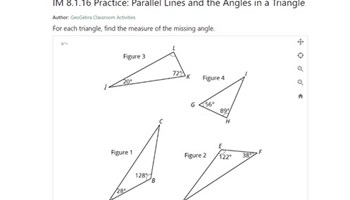
Parallel lines and the angles in a triangle
In this activity students find the missing angle in a triangle and identify angles on parallel lines.
Go to resource -
Alternate interior angles assessment activity
In this activity students identify and find the size of alternate angles.
Go to resource -
Supplementary angles
In this activity students are shown what constitutes a supplementary angle and answer a series of questions to demonstrate their understanding.
Go to resource