Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M10ST02, AC9M10ST03, AC9M10ST04
Numeracy Progression: Interpreting and representing data: P8
At this level, students are competent with comparing data distributions and are fluent in the relevant mathematical vocabulary. Extend students to work with other data displays, such as box plots, to represent continuous numerical variables. Review the distinction between continuous and discrete numerical data, referring to continuous data as 'measured' rather than 'counted'.
Teach students to construct box plots and ensure they understand the important elements of shape, centre, spread and outliers. Use worked examples to show the differences between multiple box plots displayed back to back for students to analyse and make comparisons.
Use real-world reports that use box plots, such as using your school's NAPLAN data, to analyse with your students. Ask students to communicate their findings back to the class for further discussion. This is an authentic exercise for students to engage in. Access the data from the previous year to make comparisons more relevant.
Students also work with scatterplots and examine the trends that visually emerge from these plots, such as linearity, or the direction or strength of the relationship between variables.
This topic is the steppingstone into correlation. Find interesting and engaging examples online that show odd, yet extremely strong relationships between unrelated variables on scatter plots (for example, consumption of mozzarella with attainment of civil engineering doctorates). Use these examples to reinforce that correlation does not equal causation.
Teach students to construct two-way tables and use worked examples to show students how to recognise relationships between categorical variables.
Teaching and learning summary:
- Use explicit teaching strategies and worked examples to show students how to construct box plots.
- Discuss how box plot comparisons can be made in terms of shape, spread and outliers.
- Demonstrate the effectiveness of comparing box plots side by side on the same axis and the statements that can be made.
- Show students how to create scatterplots and use worked examples to show relationships between variables.
- Use digital software to find a line-of-best-fit for scatterplots and discuss its accuracy and interpretation.
- Help students to construct two-way tables from categorical data and use worked examples to show relationship strength.
Students:
- compare data distributions for continuous numerical variables using comprehensive mathematical vocabulary
- construct box plots and can analyse shape, spread, outliers and the centre for a given context and data-set
- compare box plots side by side and draw reasonable conclusions about the datasets
- construct scatterplots noting the strength of relationship between two variables (direction, linearity, strength)
- construct two-way tables and make connections between trends or relationships between categorical variables.
Some students may:
- be adept at learning and constructing box plots, scatterplots and two-way tables, but not fully comprehend why these are used to represent data.
- have never seen these graphs in real-world contexts and will need to be exposed to relevant box plots (for example, using academic data).
- require a refresher in key vocabulary.
- be confused with percentiles and how they are represented by each marker on the box plot.
- work easily with numbers and categories but fail to understand them in a real-world context.
- confuse types of data and the appropriate forms of data display.
- find it difficult to make conclusions that are grounded in data, rather than hypotheses.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to generate box plots using digital technology.
- We will compare the centre, spread, shape and presence of outliers in the distributions.
Why are we learning about this?
You are growing up in a world that is fuelled by data. Many industries now expect their workers to be data literate and to make evidence-based decisions. Your teachers are prime examples. Behind the scenes, they are analysing data generated by your academic journey to provide the best and most consistent learning experience for each cohort and individual.
What to do
Step into the shoes of your teachers for a day and see if you can compare sets of fictional mathematics test scores!
- You are going to use spreadsheet software, like Excel, to create fictional sets of test scores. You may wish to model this on your current year level or you can make your test scores up and enter them manually. I am going to teach you how to do it automatically.
- Open up a new spreadsheet and use Row 1 to name each class with sensible titles: Class 1, Class 2, Class 3 etc. See the table below.
- The function '=randbetween(1,100)' will generate random class test scores for you. To do this, select Column A Row 2, and type in =randbetween(1,100). A number between 1 and 100 should appear. Hover the mouse at the bottom right of the cell and you will see a +. Select and pull down to proliferate the column, which is Class 1 in the example below.
- Do this for each class. You should end up with something that looks like this. It's up to you how many rows you fill, but I would suggest about 25.
Class 1 Class 2 Class 3 Class 4 Class 5 25 73 34 50 55 86 14 57 16 19 17 55 68 13 54 43 87 90 90 49 41 88 44 95 60 1 38 43 55 40 16 51 41 88 81 24 61 78 11 91 34 41 69 90 39 66 99 24 52 77 51 81 6 70 88 24 85 52 54 76 75 56 17 64 61 25 80 71 71 93 97 89 39 67 7 7 45 25 64 42 - Set up a table, such as the table above, to organise the summary statistics for each class and then calculate the mean, median, mode and range for each class.
- What do you notice? Remember the real-world context here! If you were the lead mathematics teacher for this year level, what would you think? What would you want to say at the next mathematics meeting with all class teachers?
- Let’s do further analysis by visualising this data on box plots. Select all the data and click the Insert tab.
- Expand the Charts tab, scroll down all the different types of displays and select 'box plots'. In Excel, this is called 'Box and Whisker'. This action will insert side-by-side box plots. It should look something like this.
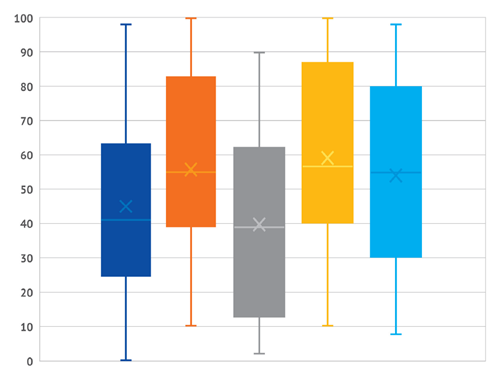
- Revisit your comments from earlier. What can you add? What needs to be adjusted?
- Now imagine you have a meeting with the head of mathematics and all the mathematics teachers; prepare a short presentation for this next meeting to reflect on the outcomes of this test.
So, is teaching for you? There’s more to it than you think!
Success criteria
- I can use technology to generate datasets and display them effectively with side-by-side box plots.
- I can make accurate comparisons of datasets, referencing the centre, spread, shape and outliers and present it in an informative manner.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Would you rather …?
In this lesson, students collect data, creating and analysing two-way tables.
Go to resource -
Construct and interpret box plots
Access this webpage for explicit guidance on teaching the construction of box plots and how to make comparisons.
Go to resource -

Data representation and interpretation
This learning sequence provides detailed guidance for teachers on how to show and engage students in the interpretation and representation of data, specifically for box plots and scatterplots.
Go to resource -
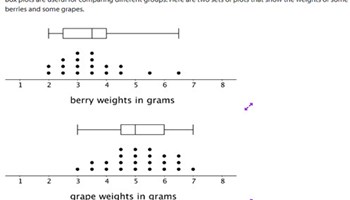
Using box plots
This interactive lesson and practice activity can be used for the construction of box plots in a real-world simulation about school students and sleep.
Go to resource -
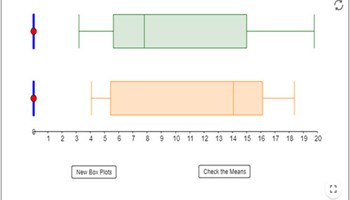
Where’s the mean?
An interactive practice opportunity about finding and comparing means of stacked box plots while considering outliers and range.
Go to resource -
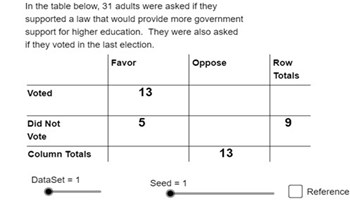
Two-way tables
This is an interactive two-way table activity where students can manipulate the dataset to observe variation in the table.
Go to resource
Assessment
By the end of Year 10, students can compare the distribution of continuous numerical data using various displays, and discuss distributions in terms of centre, spread, shape and outliers. Students can also represent the distribution of data involving two variables, using tables and scatter plots, and comment on possible association.
-
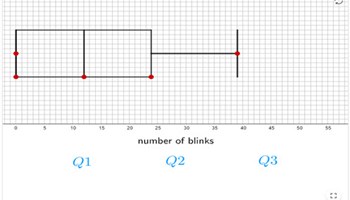
Lesson: box plots
This resource is an interactive assessment activity on box plots with answers available to teachers and students.
Go to resource -
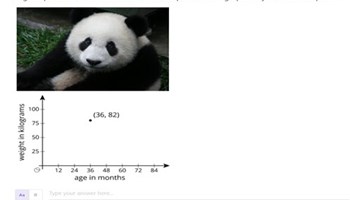
What a point in a scatterplot means
This interactive resource prompts students to question and consider the main elements of scatterplots and how to interpret them in relation to context.
Go to resource -
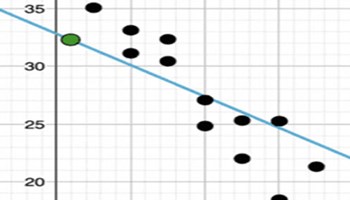
Describing trends in scatterplots
This interactive activity or assessment is specifically designed to test students on trends that may be found in scatterplots between variables.
Go to resource -

Two-way tables
This is an interactive two-way table activity where students can manipulate the data-set to observe variations in the table.
Go to resource -
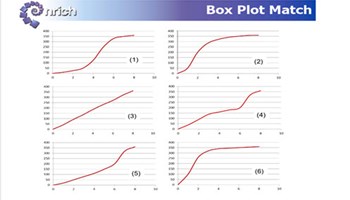
Box plot match
Students are presented with different frequency graphs and are asked to match them to their corresponding box plots.
Go to resource