Units of measurement for capacity
Year level: 6
Strand: Number / Measurement
Lesson length: 90–100 mins
In this lesson, students learn about the units of measurement for capacity and how to convert between them. They then develop a set of instructions that explains how to convert between the units of measurement without a calculator.
The lesson offers a real-world context for extending place value beyond thousands for a purpose.
This lesson is the second of 5 lessons that connect the cross-curriculum priority of Sustainability with Number, Measurement and Statistics. It can also complement the science content description. AC9S6U04
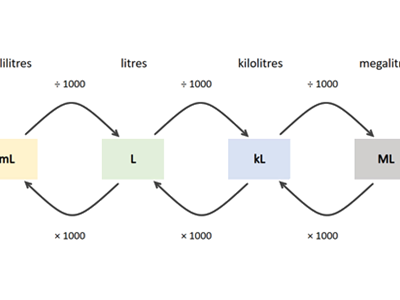
Curriculum information
Achievement standard
Students use all 4 operations with decimals and connect decimal representations of measurements to the metric system. Students convert between common units of length, mass and capacity.
Content descriptions
Convert between common metric units of length, mass and capacity; choose and use decimal representations of metric measurements relevant to the context of a problem. AC9M6N06
Multiply and divide decimals by multiples of powers of 10 without a calculator, applying knowledge of place value and proficiency with multiplication facts; using estimation and rounding to check the reasonableness of answers. AC9M6M01
General capabilities
Numeracy
Cross-curriculum priorities
- Sustainability (SF2)
Assessment
Refer to the exit ticket on slide 11.
1. Does the capacity of an object change when we convert the units of measurement from one to another?
Yes or No
2. 3 litres of water is equivalent to:
a) 003 kilolitres
b) 3000 kilolitres
Expected answers:
- No (the units of measurement are equivalent expressions for the same capacity).
- a). 0.003 kilolitres
Prerequisite student knowledge and language
- Read, write and interpret numbers up to a million
- Multiply and divide natural numbers and decimal numbers by multiples of powers of 10 without a calculator
- Read, write and interpret decimal numbers up to 1000ths
- Know the number of days in a week, month and year
- Read and interpret a table
Language
- millilitres, litres, kilolitre, megalitre
- convert
- equivalent expression
- move the digits ‘_’ places to the left/right
- tenths, hundredths, thousandths
Areas of challenge
Some students may:
- be challenged reading, speaking and interpreting numbers up to and beyond a million
- be less proficient working with decimals up to thousandths
- have difficulty understanding that the measurement number will get smaller when converting from a smaller unit of measure (e.g. mL) to a larger unit of measure (e.g. L), and vice versa.
What you need:
Lesson plan (Word)
Teacher’s slides (PowerPoint)
Converting units of measurement sheet (Word)
Practice questions: Mild, Medium and Spicy (Word)
Learning goals
Learning intention
We are learning about the units of measurement for capacity and how to convert between them, with and without a calculator.
We are practising to reading, speaking and interpreting numbers beyond 1000 in real-world contexts.
Success criteria
By the end of this lesson, students can:
- name four common units of measurement for capacity
- convert between the units of measurement for capacity using a calculator
- convert between the units of measurement for capacity without a calculator
- read, speak and interpret numbers beyond 1000 in real-world contexts.
Why are we learning about this?
Converting measurements to the same unit of measure provides a common language for working with and comparing the sizes of the measurements (smaller, bigger, the same size).
Shortening a measurement number by converting it to an equivalent unit of measure can make it easier to read and work with (easier to read 58 millilitres than 0.058 litres).
Learning hook 10 mins
- Introduce the lesson theme by asking students to think about objects that have the following units of measurement for capacity: millilitres (mL), litres (L), kilolitres (kL) and megalitres (ML).
- Project slide 4 of the teacher’s slides.
Ask students to write down examples of objects that they think might have the 4 listed units of measurement.
Images of relevant objects have been included on the slide as a hint.
Collect students’ responses via a mini whiteboard, survey or as a whole-class discussion.
- Which of the units of measurement do you think are used for smaller/larger amounts of liquid? Why do you think that?
- Can you think of another unit of measure that uses the prefix ‘milli’ or ‘kilo’?
(milligram, millimetre, kilogram, kilometre) - How many millilitres do you think might be in 1 litre? Explain your reasoning.
- How many litres do you think might be in 1 kilolitre? Explain your reasoning.
- What about a megalitre, how many litres or kilolitres might it have?
Encourage students to consider what a megalitre could represent and explain their reasoning. (They will find out the size of one megalitre during this lesson.)
Explore 70–80 mins
Introduction
- Use either the class’s calculations from the previous lesson ‘How much water does our class use?’ or the sample data below (also on slide 5), to review place value and large number names, before moving to converting between units of measurement.
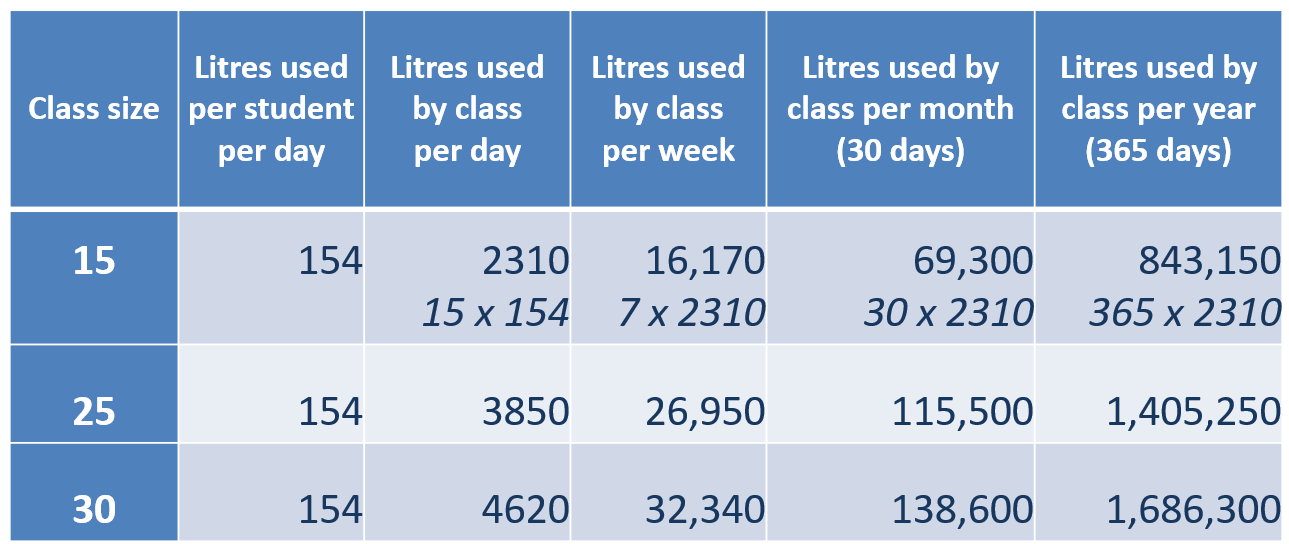
Slide 5
Display slide 5 and have students individually consider what is being shown in this table. After a pause, ask students to explain their understanding of what the table is showing to another student or discuss in groups. Check students’ understanding and provide additional support as required.
Working in pairs, ask students to take it in turns to pick a number from the table and say it out loud to their partner. Challenge them to see if between them they can say every number in the table.
Slide 6 includes a summary table of large numbers up to 1 trillion, to scaffold this activity if needed.
|
Name |
Amount |
Number of zeros |
Groups of (3) zeros '000' |
|
Ten |
10 |
1 |
|
|
Hundred |
100 |
2 |
|
|
Thousand |
1,000 |
3 |
1 |
|
Ten thousand |
10,000 |
4 |
|
|
Hundred thousand |
100,000 |
5 |
|
|
Million |
1,000,000 |
6 |
2 |
|
Billion |
1,000,000,000 |
9 |
3 |
|
Trillion |
1,000,000,000,000 |
12 |
4 |
- Explicitly teach how to convert from one unit of measurement to another and provide several examples of how to apply this. (Diagram is on slide 7 and in Converting units of measure sheet.)
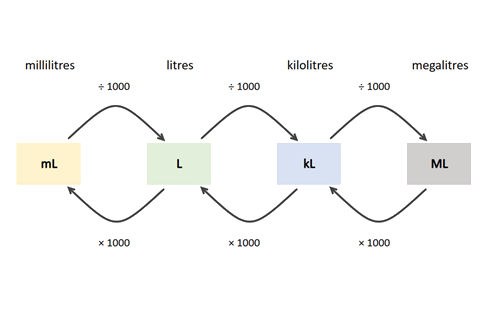
Slide 7
Start by checking that students know how to use the conversion table.
A kettle holds 2.5 litres of water, how many millilitres is this?
- Locate the units of measurement you have on the diagram (litres).
- Locate the units of measurement you want to convert to the diagram (millilitres).
- Which of the two arrows goes in the direction you are converting to (x 1000).
- Anticipate: will the number be larger or smaller after the conversion?
- Do the calculation (2.5 x 1000 = 2500 millilitres).
- Check your answer, does it make sense?
Distribute Converting units of measurement sheet and work through the additional examples on slide 8 with the whole class, as needed. Ask students to write down their anticipated answer before working through the examples as a class.
- Introduce the task on slide 9, explaining that the task is only about units of measurement for capacity.
Develop a set of instructions that explains how to convert between units of measurement without a calculator. Include at least two examples – one converting from a smaller unit of measure to a larger one, and the other converting from a larger unit of measure to a smaller one.
- Check to see if students have any additional clarifying questions before starting on the task.
- Encourage students to plan their approach to the task individually before sharing their ideas with another student. Make calculators available so that all students can complete the calculations and observe the pattern of the digits moving 3 places to the left or right when converting between units of measurement. Once students understand the pattern, they should continue without a calculator, and then use one to check their answer as needed.
- Practice questions: Mild, Medium and Spicy includes a range of conversion questions for students to build their understand of the process before developing their own set of instructions. The questions have been organised into three levels of difficulty:
- Mild (involves × 1000)
- Medium (involves ÷ 1000)
- Spicy (a combination of x 1000 and ÷ 1000).
Students are not expected to work through all questions, rather they select from the range of questions available until they feel confident they understand the process. Students who can correctly answer the mild and medium level questions, especially questions 5, 6, 11 and 12, are demonstrating a sound understanding of conversion between units of measurement for capacity and the corresponding place value.
- Questions and prompts (also on slide 10):
- How many places do the digits move when you ‘× 1000’? Why might that be?
- How many places do the digits move when you ‘÷ 1000’? Why might that be?
- What calculation has been applied when the digits move to the left. Is it × 1000 or ÷ 1000? How do you know?
- When converting a smaller unit of measure, like millilitres, to a larger unit, like litres, does the size of the number increase or decrease?
- How could you convert from litres to kilolitres, or kilolitres to litres, without using a calculator?
Differentiation (support) – start with litres and millilitres, and calculations involving × 1000.
Have students use a calculator so that the focus is on building conceptual understanding of the process of converting from one unit to another, rather than performing the multiplication accurately.
- How many millilitres in a litre?
- If I have 1 litre, how many millilitres is that? Repeat for 2 litres, 3 litres and so on. Can you see a pattern between the number of litres and corresponding millilitres?
- If I have 2.5 litres, how many millilitres is that? (Encourage them to make an estimate before using the calculator.)
- If I have 0.5 litres, follow the pattern to work out the corresponding millilitres.
Repeat this process for going from millilitres to litres (÷ 1000).
Differentiation (extend)
- How many places, and in what direction, would the digits move when converting from megalitres to millilitres or vice versa?
- The population of Australia is currently around 26,170,000. Make some estimates and calculate the water used at home per day, week and month.
Make an approximate calculation of the amount of water you have used at home since you were born. State your assumptions.
Summary and reflection 10 mins
- Start by having students work in pairs to share their instructions for converting from one unit to another.
- Basing the order of presentations on observations of students’ work, ask students to share with the class their instructions for how to convert between units of measurement without a calculator.
- Invite students to ask clarifying questions.
- As students share their instructions, write key points on the board and add and refine along the way.
Some guiding questions might be:
- Can you link the pattern you noticed to the calculation being made?
- When did the digits move to the left/right?
Are there any similarities you see between the work we’ve just done and other measurements?