Osprey bird dimensions
Year level: 5 / 6
Strand: Statistics / Measurement
Lesson length: 75 mins
In this lesson, students investigate measurement data related to the osprey. Students represent and interpret data related to wingspan and body length. They investigate patterns in data to describe any relationships.
This lesson is the third in a series of six lessons that connect the cross-curriculum priority of Sustainability, Statistics and the Science learning area: Science as a human endeavour. AC9S5H01, AC9S6H01 and AC9S5H02, AC9S6H02.
This lesson was developed in collaboration with Conservation Without Borders. Data and information provided by Tweed Valley Osprey Project.
Curriculum information
Achievement standard
By the end of year 5, students choose and use appropriate metric units to measure the attributes of length, mass and capacity, and to solve problems involving perimeter and area. They interpret and compare data sets for ordinal and nominal categorical, discrete and continuous numerical variables using comparative displays or visualisations and digital tools. They identify the mode and interpret the shape of distributions of data in context. They compare distributions of discrete and continuous numerical and ordinal categorical data sets as part of their statistical investigations, using digital tools.
By the end of year 6, students use all four operations with decimals and connect decimal representations of measurements to the metric system. They compare distributions of discrete and continuous numerical and ordinal categorical data sets as part of their statistical investigations, using digital tools.
Content descriptions
Students acquire, validate and represent data for nominal and ordinal categorical and discrete numerical variables, to address a question of interest or purpose using software including spreadsheets; discuss and report on data distributions in terms of highest frequency (mode) and shape, in the context of the data. AC9M5ST01
Students choose appropriate metric units when measuring the length, mass and capacity of objects; use smaller units or a combination of units to obtain a more accurate measure. AC9M5M01
Students interpret and compare data sets for ordinal and nominal categorical, discrete and continuous numerical variables using comparative displays or visualisations and digital tools; compare distributions in terms of mode, range and shape. AC9M6ST01
Students convert between common metric units of length, mass and capacity; choose and use decimal representations of metric measurements relevant to the context of a problem. AC9M6M01
General capabilities
Numeracy
- Interpreting and representing data (Level 4)
Digital literacy
- Investigating: Interpret data (Level 4)
Cross-curriculum priorities
Sustainability
- Futures (SF1)
Assessment
Ask students to communicate their findings (slide 11). Do students back up their conclusions using data and visual representations? Can students make relevant and accurate conclusions about the data? For example:
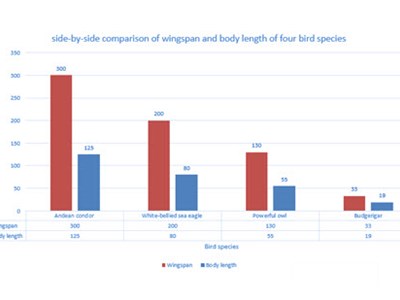
- The wingspan of the Andean condor, white-bellied sea eagle and powerful owl, which are all raptors, is approximately 2.5 times bigger than their body length.
Keep the student completed sheets as a record of their learning. Have those students that used a spreadsheet save the digital versions of their graphs. Use these to assess their progress in use of spreadsheeting software such as Excel (MS) or Numbers (iOS). Create a class checklist to assess students’ proficiency in the use of a spreadsheet to analyse and visualise data.
Can students give reasons for their choice of chart used to represent the information? For example:
- A side-by-side graph is useful to represent two values for comparison.
- A scatter plot is useful to visualise and observe any relationships between two variables.
Areas of challenge
Some students may:
- have difficulty transferring data in a table to a visual representation such as a chart
- have limited familiarity with working with data using a spreadsheet
- require support to interpret different charts and to choose the most suitable chart to represent a data set.
Prerequisite student knowledge and language
Prior to this lesson, it is assumed that students have knowledge of:
- interpreting information in a table
- representing data in column graphs
- different ways to visualise data other than a column graph.
It is also assumed students are familiar with the terms:
- wingspan – the distance from the tip of one wing to the tip of the other wing when fully extended, often used to describe the size of birds
- side-by-side column graph – used to compare the values of multiple datasets by displaying vertical bars side by side.
What you need:
Lesson plan (Word)
Teacher’s slides (PowerPoint)
Wingspan and body length data (Excel)
Wingspan and body length data set-up (Excel)
Sacha Dench profile poster (PDF)
Access to computer/tablet and spreadsheet software such as Excel (MS) or Numbers (iOS)
Measuring equipment such as rulers (30 cm or preferably metre), tape measure or string
Learning goals
Learning intention
- We are learning about ways to represent and report on real scientific data.
- We will use the research tasks to develop our data skills including using a spreadsheet and creating charts.
Success criteria
By the end of this lesson, students can:
- apply place value to measurement problems
- interpret data presented as a table
- use a chart to display acquired data
- visually represent and report on acquired data.
Why are we learning about this?
The work done by research team helps us to learn more about the natural world. Using the context of contributing to a research team gathering data, we can identify patterns, analyse trends, and observe changes over time. Exploring basic technologies, such as GPS tracking used by scientists, enhances our understanding of data collection and analysis. Additionally, mastering the creation and interpretation of data displays is a crucial skill, as it allows us to communicate information effectively through visual means.
Learning hook 5 mins
- Download and use the teacher’s slides to accompany your teaching.
- Use slides 3–4 to view data about the osprey. Ask students to interpret the information and discuss measurements of interest.
- Refer to the two multiple choice questions that relate to measurement of mass. View the notes for support.
- Explain that today we will be looking at data relating to a bird’s wingspan and body length, beginning with the osprey.
Explore 60 mins
Introduction (15mins)
- View data in the table on slide 4 for the osprey’s wingspan and body length, each given as a range. So that students get a sense of the osprey’s large wingspan compared to its body have students measure their arm span and height.
- Organise students to work in pairs to measure each other’s arm span and height (slide 5). Provide measuring equipment.

Slide 5
- Students can record their measurements in their own table or into a shared class table. Alternatively open the spreadsheet Class arm length vs height and project the spreadsheet on a whiteboard. The scatter plot is automatically set up to populate as students’ data is entered. Interpret the scatter plot graph. Explain that a scatter plot is a graph that displays the relationship between two continuous variables, showing individual data points as dots. In our example, the variables are arm span and height.
- Discuss any patterns that students notice. Ask students, ‘How does your arm span compare to your height?’ Generally, the measurements of a person’s arm length and height are a close match.
- Compare these measurements to those of the osprey. Students should be able to estimate that the osprey’s wingspan is about 3 times its body length (based on using the figures rounded to 180 and 60) – much different to humans.
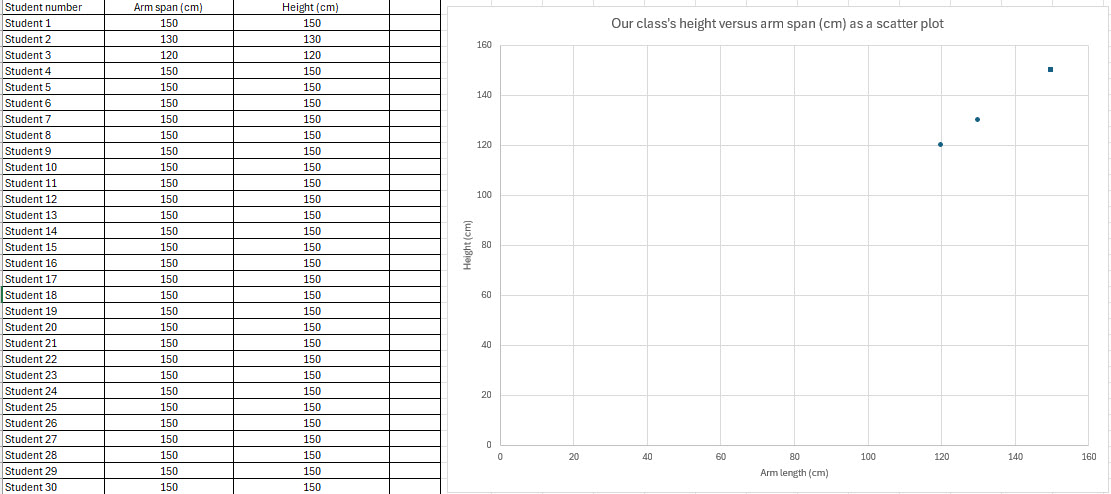
Image: Excel spreadsheet: Class arm length vs height
Practical activity (45 min)
- Provide a table of data from the Body length versus wingspan worksheet for students investigate and represent visually (slide 6). The worksheet has two different partly completed graphs for use by students who require support. Students select a graph type and use data from the table to complete the graph.
Ideally students use a spreadsheet to organise the data and create a graph rather than drawing a graph using pencil and paper.
- For students familiar with using a spreadsheet provide the spreadsheet Wingspan and body length data.
- Consider modelling how to create each type of graph. Use the spreadsheet Wingspan and body length data set up. This includes a table already set up for data entry with the graph auto-generating. Two types of charts are provided. Note: even after a class demonstration, some students may need further help with Excel (MS) or Numbers (iOS) to create their graphs.
- Observe how students are approaching the task. Support them with enabling and extending prompts, as required.
Differentiation (enable)
- How can you represent the data? How do you show this data using a side-by-side column graph (slide 7)?
Differentiation (extend)
How might you compare the two variables of wingspan and body length? What type of graph can you use? Can you show body length along the x-axis and wingspan along the y-axis? What patterns do you notice?
Summary and reflection 10 mins
Display slides 8 and 10 and ask students to describe their findings:
- Review similarities and differences in representing data as side-by-side column graph or as a scatter plot.
Use questioning to prompt students to describe the relationship between body length and wingspan.
- For Andean condor, white-bellied sea eagle and powerful owl, which are all raptors, the wingspan is approximately 2.5 times bigger than the body length.
- Students may notice that the four points roughly make a straight line.
Ask students to use their graph to predict a bird’s wingspan.
- If a bird had a body length of 100 cm what might you expect its wingspan to be? Why? (They may suggest 250 cm if it follows the pattern). Use teacher modelling to show that as 2.5 x 100 = 250
- What about a bird with a body length of 40 cm? What would you expect its wingspan to be? (Students may suggest about 100 cm if it follows the same pattern.) Use teacher modelling to show that as 2.5 x 40 = 100