Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M9A02
Numeracy Progression: Number patterns and algebraic thinking: P9
At this level, students move beyond expanding and factorising linear expressions, such as 3(2x – 1) or 4x + 6, to working with monic quadratic expressions (that is, where the coefficient of the square term is 1). This involves expanding expressions of the form (x + a)(x + b), such as (x + 2)(x – 8), and factorising expressions of the form x2 + mx + n, such as x2 – 4x + 3.
While students will have previously worked with squaring numbers and squaring in area calculations, this may be the first time they regularly come across the term ‘quadratic’ in reference to algebraic expressions. The abstract representation of these expressions, in expanded and factorised forms, may seem daunting. Small, step-by-step explicit instruction using concrete manipulatives (algebra tiles or area models) or digital tools is helpful for this topic.
It is important to consistently use the language and conventions of algebra when developing and demonstrating various concepts and processes, so that students progressively become more comfortable with formulating and manipulating quadratic expressions. They can then start to make connections from learning abstractly to systematically exploring and identifying patterns and relationships between expansion and factorisation based on
(x + a)(x + b) = x2 + (a + b)x + ab, where a and b are integers.
By the end of this topic, students should be able to identify x2, x and constant terms with integer coefficients, in expanded or factorised forms of monic quadratic expressions, and move between equivalent expanded and factorised representations.
Teaching and learning summary:
- Use worked examples to show the combinations of binomials so that students can practise expansion skills.
- Show the process for factorising monic quadratic expressions.
- Use concrete manipulatives and digital tools to aid explanation.
- Ensure students can expand (x + a)(x + b) and factorise
x2 + mx + n , where m and n are integers.
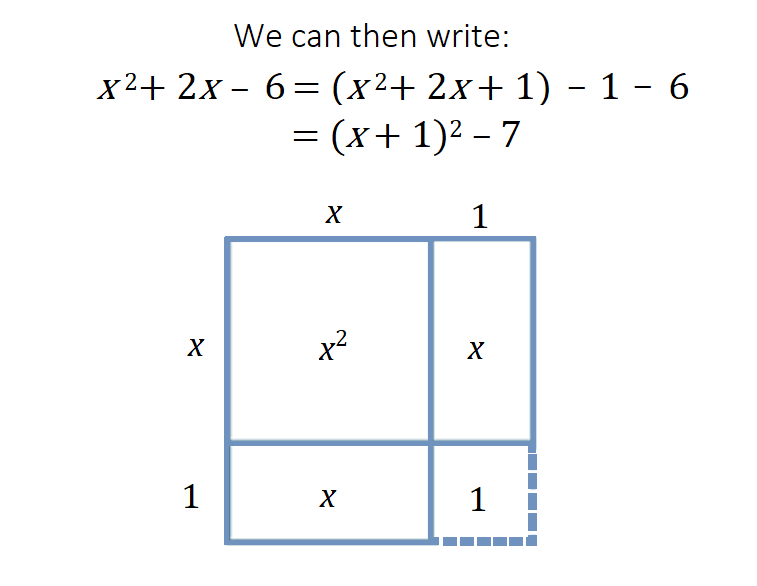
Students:
- are familiar and comfortable with the conventions and language of quadratic expressions
- can formulate and manipulate a variety of linear and quadratic expressions
- can expand binomial products
- can factorise monic quadratic expressions
- make connections between factorisation and expansion in relation to monic quadratic expressions.
Some students may:
- not understand the convention of implied multiplication. This could mean that they still need to learn that 6x stands for 6 multiplied by x or 6 lots of x, or that ab stands for a × b.
- be incorrectly calculating expressions involving negative integers, for example, thinking –2 × –3 = –6 rather than +6, or with simple algebraic operations such as the combination of like terms.
- not correctly or completely apply the distributive property when expanding the product of two binomial expressions, such as simply missing out middle terms, incorrectly thinking (x + 3)2 = x2 + 9.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I am learning to recognise quadratic expressions and describe their terms.
- I am learning to expand the product of two binomial expressions.
- I am learning to factorise simple quadratic expressions.
Why are we learning about this?
Quadratic functions and their rules can be used to model situations and solve problems involving curves, area, patterns and movement. Formulating and manipulating quadratic expressions provides general ways to describe and understand these functions, expanding the range of practical problems we can solve.
What to do
Practise expanding
- Use the interactive Quadratics - expand brackets – GeoGebra to practise expanding. Tick the ‘show working’ box and set the sliders for a and c to 1.
- Use any method to expand each of the following:
(x + 3)(x + 5) (x + 3)(x – 5) (x – 3)(x + 5) (x – 3)(x – 5) - Repeat these combinations for several other pairs of numbers, and in each case compare the x term and the constant term in the expanded form with the two numbers in the factorised form.
- Describe any patterns you notice.
- See if you can use your pattern to expand the following in one step:
(x + 5)(x + 2) (x + 4)(x – 6) (x – 3)(x + 7) (x – 8)(x – 1)
Practise factorising
Use the interactive Quadratics factorisation game – GeoGebra to practise factorising (move the sliders to show what you think the answer is, and then check it using the 'check answer' button).
Success criteria
- I can identify and describe the terms in a quadratic expression.
- I can expand the product of two binomial expressions.
- I can factorise monic quadratic expressions.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

AMSI: Factorisation
This teacher guide steps teachers through the concept of factorisation for Year 9. Worked examples and exercises with answers are also provided.
Go to resource -

Introduction to algebra
Use this interactive site to study quadratic functions, comparing them to linear or exponential growth while examining the properties of different algebraic forms.
Go to resource -

Factorising and solving quadratic equations
This is an all-encompassing resource that provides teacher guidance, student misconceptions, worked examples and multiple examples.
Go to resource -
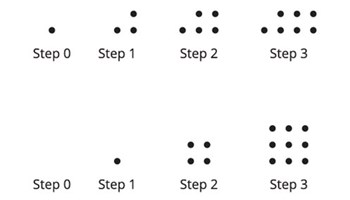
How does it change?
This resource connects quadratics with pattern and shape. It uses a visual approach to systematically formulating quadratic expressions. It includes teacher guidance, a lesson plan, student-facing material and answers.
Go to resource -
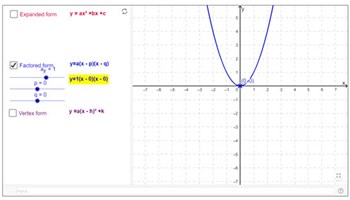
The three forms of quadratic functions
Students interact and explore three forms of quadratic functions by varying inputs to see the effect on the function in question. Note that this task is best suited to students who enjoy being extended.
Go to resource -
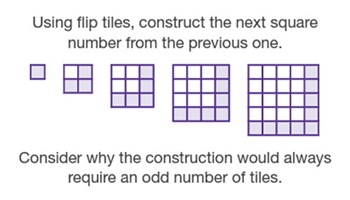
Patterns and algebra: Year 9
Use this resource to access information on content descriptions on this topic, advice on how to engage learners, and student activities on simplifying expressions, expanding binomials and quadratic equations.
Go to resource
Assessment
By the end of Year 9, students can simplify algebraic expressions, expand binomial products, and factorise monic quadratic expressions.
-

Quadratic quiz
This digital interactive is a 20-question quiz where students use one value of x to practise various binomials.
Go to resource -

How does it change?
This resource connects quadratics with pattern and shape. It uses a visual approach to systematically formulate quadratic expressions. It includes teacher guidance, a lesson plan, student-facing material and answers.
Go to resource -

Patterns and algebra: Year 9
Use this resource to access information on content descriptions on this topic, advice on how to engage learners, and student activities on simplifying expressions, expanding binomials and quadratic equations.
Go to resource