Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8ST03
Numeracy Progression: Interpreting and representing data: P7
At this level, students focus on understanding that random samples chosen from large populations can show quite different distributions and proportions when compared with each other. Students make connections when different sample sizes are or can be responsible for this effect, which can be shown numerically or visually.
Students use large, real-world data and population samples from the ABS, for example, and experiment with sample size. Students investigate variations of the same sample using digital tools. This allows for easy and repetitive simulations of measurements such as relative frequencies, mean and median and the effect on the central tendency when data is removed from or added to a data set.
Teaching and learning summary:
- Discuss the effect of different-sized sampling from large populations.
- Show how different samples, from the same population, can look different.
- Show the effect on statistical analysis, such as mean, median and range, when different samples and different samples sizes are used.
- Show the effect on central tendency when data points are added or removed from the data set.

Students:
- know and can explain some of the problems when sampling from a large population
- investigate and compare different sample sizes from the same population in relation to mean, median and range
- investigate the result when data is removed or added from a data set.
Some students may:
- not realise that a sample size from a large population is used to make generalisations about the populations.
- not understand that two different samples from the same population may show variable results, such as mean and range.
- underestimate the differences between very small samples sizes versus very large samples sizes.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I am learning how taking different samples from a population affects sample statistics.
- I will use different samples from a population to explore if the mean, median or range vary.
Why are we learning about this?
What we choose to believe or buy can be influenced by the information we receive. Data can often be easily distorted (misrepresented) by either omission or incorrect statistic used (for example, when the mean is used when the median should have been used).
It is often impractical to collect all the data for a population so sample statistics are used as an estimate for the population.
What to do
A sporting team pays their players a salary each season. To improve the team’s finishing place on the ladder and attempt to win a premiership, management decide to bring in a star player for the second season.
Salary data
Season 1 (in $)
80,000 110,000 145,000 153,000 162,000 226,000 234,000 285,000 290,000 305,000
Season 2 (in $)
80,000 110,000 145,000 153,000 162,000 226,000 234,000 285,000 290,000 305,000 750,000
Questions
- For each season, calculate the mean, median and range of players’ salaries.
- Which statistic do you think management would use if trying to justify bringing in a star player but downplaying the cost involved?
Success criteria
- I can calculate statistics for a given data set to create information.
- I can choose appropriate statistics to accurately represent data.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Shooting 3-pointers: Part 1
In this lesson students are guided through solving a problem using mathematical modelling.
Go to resource -

Shooting 3-pointers: Part 2
In this lesson, students conduct a statistical investigation.
Go to resource -
Are you average? (Part 3)
In this lesson students analyse and report on the distribution of their data for the ‘whole’ school drawing conclusions with respect to different sampling techniques and whether methods chosen were fair and considered.
Go to resource -
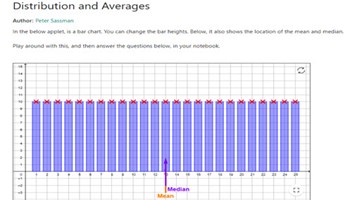
Distribution and averages
Change the height of the bars and see how it changes the mean and median.
Go to resource -

Estimating population measures of centre
This resource for teachers and students encourages questioning on different populations and when different samples are taken from the same population. How does variability affect measures of centre?
Go to resource
Assessment
By the end of Year 8, students can compare the variation in distributions of random samples of the same and different size from a given population with respect to shape, measures of central tendency and range.
-
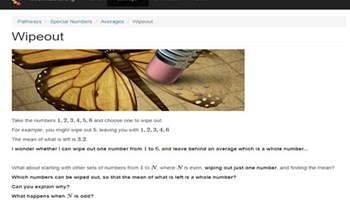
Wipe out
Can you ‘wipe out’ a number in a list so that the remaining numbers have a specified mean?
Go to resource -
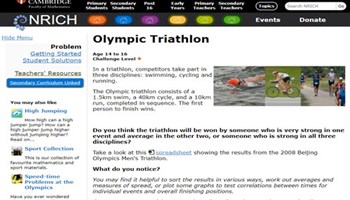
Olympic triathlon
A look at average times in different events compared to overall averages. Create a task on sample size from this worksheet of real-world data available in spreadsheet form or printable PDF.
Go to resource -

Picturing the world
A challenging exercise that could work well for a group assessment in class. Students use big data and are prompted to use their proportional reasoning skills to make generalisations about the world we live in.
Go to resource -

Sampling and estimating: counting trees
This lesson is designed to assess students’ ability to estimate a population using proportion and sampling techniques.
Go to resource