Expected level of development
Australian Curriculum Mathematics V9: AC9M8M02
Numeracy Progression: Understanding units of measurement: P9
At this level, students further develop their understanding of volume and capacity of right prisms by developing formulas, taking measurements and investigating, making approximations and solving problems in many contexts.
Time should be taken to review the concept of volume/capacity and the definition of a right prism – a 3D object with plane, rectangular faces and bases that are aligned above each other.
Concrete objects, such as unit cubes and dynamic geometry software, can support students’ understanding. Students solve real-world problems using many examples from everyday life. Provide opportunities for students to investigate volume and capacity in different ways. For example, if a washing machine takes x minutes to fill, what is the capacity of the drum?
When introducing a new prism, students should be shown the object in a variety of orientations. Demonstrating how the cross-section is identical along the length (or height) of the shape can be done by cutting a plasticine model.
Introduce the formula for the volume of prisms as ‘area of the cross-section × length (height)’. Encourage students to identify the shape of the cross-section, calculate the area and then multiply this by the length (or height).
When solving and answering problems, students should choose the appropriate measurement to measure volume and surface area. Give students opportunities to convert the same-shaped objects from the very small (a model of a prism) to to the very large (similar-shaped real-life example). This will support and develop student understanding of the selection of an appropriate unit of measurement for area and volume. It also initiates thinking in the idea of scaling.
Teaching and learning summary:
- Build on students’ understanding of volume and capacity.
- Discuss what a right prism is – constant cross-sectional area – and use real-world examples.
- Introduce the formula for the volume of a right prism – cross-sectional area × height.
- Discuss the meaning of the prefixes – milli, centi, kilo, mega.
- Relate to the decimal system.
- Discuss when to use cubed units and why.
- Discuss how to convert from one unit to another for length/height and for volume.
- Solve problems involving converting units.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
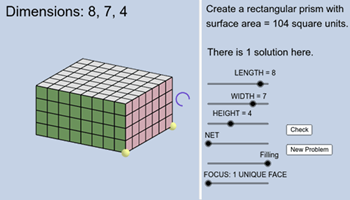
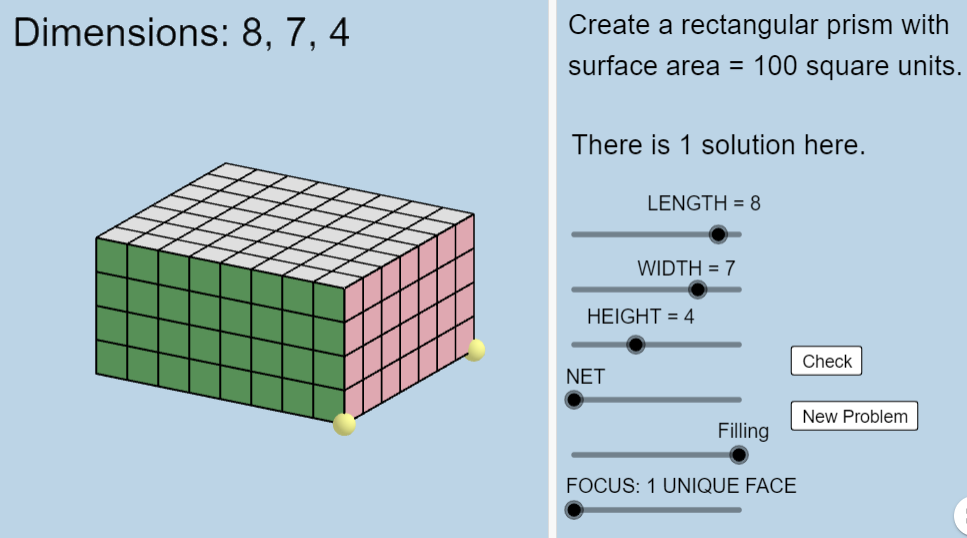
Volume of prisms
This resource focuses on the volume of rectangular prisms and the units of capacity. It gives detailed explanations of the curriculum content, worked examples and assessment questions.
Go to resource -
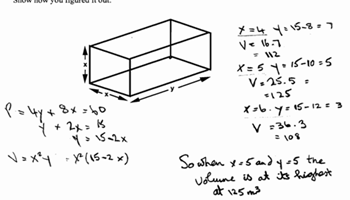
Packing a truck
This task asks students to pack a truck with boxes in an efficient way. The resource includes a lesson plan and sample student work.
Go to resource
