Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8M03
Numeracy Progression: Understanding units of measurement: P9
At this level, students recall and revise circumference, radius and diameter from Year 7. They understand the relationships between these measures and can use relevant formulas to solve problems.
Students are introduced to the formula for the area of a circle and make calculations using the correct units for different and practical contexts.
They must become familiar with mathematical terminology when working with circles. They need to understand the number π, or in an approximate form (≈ 3.14 rounded to two decimal places) and to know how to write answers in both forms. Show students how to use the π function on a calculator and ensure students feel comfortable to leave solutions in terms of π knowing that it is not a whole number or a rational number.
Investigations relating to the area of a circle could be bolstered by exploring other ways to approximate a circle’s area; for example, using a grid to make close measurements. Students could explore how the formula of the area of a circle was derived.
Teaching and learning summary:
- Revise circles and their vocabulary – radius, diameter, circumference and pi (π).
- Investigate the relationship between the radius and the diameter.
- Investigate the relationship between the diameter and the circumference.
- Use concrete materials, such as measuring the outside of a circle using string and making approximations on a grid to support students’ understanding of the relationships between the circumference, diameter, radius and area.
- Use the relationships between circumference, diameter, radius and area to form formulas for the circumference.
- Investigate the area of a circle and derive the formula.
- Use the formulas for the area of circles to solve practical problems.
- Identify and demonstrate the significance and uses of circles in the real world.

Students:
- identify and name the parts of a circle, including circumference, diameter and radius
- understand the significance and meaning of the symbol π as the ratio between the circumference and diameter of a circle
- revise that π is an irrational number and that a decimal or fraction is only an approximation of its exact value
- revise and use the relationships between the radius, diameter and circumference
- use a formula to find the area of a circle or sector
- know the units of measurement for the area of a circle
- apply the formulas for the area and circumference of a circle to solve practical problems.
Students may:
- confuse radius and diameter. Be explicit about using correct vocabulary. Have a list of common terms displayed to assist students.
- confuse the formulas for circumference and area.
- not appreciate that π is a number.
- use the wrong measurement. Support students to identify the diameter and radius of each circle and which measurement is required to solve problems.
- confuse square numbers – students often multiply by two instead of multiplying the number by itself.
- have difficulty in leaving answers in terms of π, preferring rounded decimals. Note: suggesting students always use 3.14 to represent π may lead students to think that π = 3.14.
- see π as a variable and substitute 3.14 for that variable.
- have difficulty in relating circumference to the distance around a circle. Make explicit that circumference is another word for perimeter.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to identify the features of a circle such as circumference, area, radius and diameter.
- We are learning to apply the formula to solve the circumference of a circle.
- We will understand irrational numbers, including π.
Why are we learning about this?
If you can build understanding and knowledge of the correct formula for measuring circles and how to approach the same problem in different ways, you can choose the best method to apply to circle problems whether they are from your textbook, worksheets or circular problems in the world around you.
What to do
- Find a spare piece of grid paper at home, or ask your teacher to provide you with some. If you have different kinds of grid paper that vary in size of the squares, then all the better.
- Use a compass to draw a circle with a diameter of 10 cm. If you don't have a compass, see if you can find a circular object to draw around on your grid paper, but make sure you measure the radius of the circle.
- Using the grid paper and a ruler, figure out how many grids exist in 1 cm2.
- Count the number of 1 cm2 squares there are in your circle.
- You might need to estimate the squares that border the edge of the circle by adding up part-squares to approximately 1 cm2.
- Using another sheet of paper, calculate by hand the area of your triangle using the area formula for a circle. Remember your radius will either be 10 cm or it might be something else if you used an object to draw your circle. Use cm2 for the units.
- Compare your calculated results with your grid approach. How close are you? Can you get closer? What if you used larger or smaller squares in your grid approach? What result do you get if you used mm2?
Success criteria
I can:
- apply the correct formula for the area of a circle
- understand and utilise π
- identify and name parts of a circle
- use different approaches to solve problems.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Circles
This resource focuses on the features and area of a circle. It gives detailed explanations of the curriculum content, worked examples and assessment questions.
Go to resource -
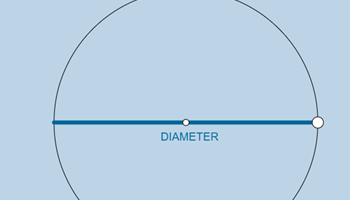
True meaning of pi
This activity gives a visual representation of the relationship between the circumference and diameter of a circle.
Go to resource -
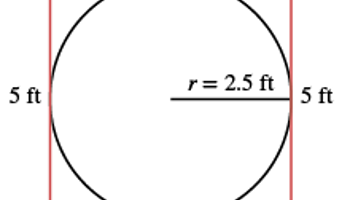
Measuring circles
This unit consists of several lessons that introduce the geometry of circles. They explore the radius, diameter and area and how to apply this knowledge to solve problems. (Note: some of the units used are imperial, not metric.)
Go to resource -

Using properties of a circle to solve problems
This resource describes how the formulas for the surface area and volume of a cylinder are derived, shows a worked example and sets some problems for students to work through.
Go to resource -

Circumference
A series of inquiry-based lessons about the relationship between the diameter and circumference of a circle.
Go to resource