Expected level of development
Australian Curriculum Mathematics V9: AC9M7SP03
Numeracy Progression: Interpreting and representing data: P7
At this level, students will describe translations, reflections and rotations and identify line (mirror) and rotational symmetries. They will extend their understanding of transformations through exploring transformations on a Cartesian plane.
Demonstrate transformations individually before showing students how they can be combined.
When introducing the Cartesian plane, show students that they should focus on one point of the shape and how that point will move under the transformation. Then extend that to other points on the shape. Students understand that a reflection will flip the shape along the axis of symmetry whereas a translation will move the shape left, right, up or down but will not flip it.
The use of mirrors and other concrete materials will allow students to develop the necessary visual and spatial skills for this topic.
This topic links to plotting coordinates on the Cartesian plane, equations of a line (for symmetry and mirror lines).
Teaching and learning summary:
- Build on students’ previous knowledge of transformation – translation, rotation, reflection.
- Translations (moving left, right, up or down).
- Reflections (flipping over the x- and/or y-axis).
- Rotations (turning an object in 90° multiples clockwise or anticlockwise).
- Identify line (mirror) and rotational symmetries.
- Revise the vocabulary of transformations and how to describe them.
- Describe two-step transformations.
- Apply transformation to a Cartesian plane and look at the effect of transformations on coordinates.
- Use transformations to create patterns.
- Identify symmetry in shapes and patterns – both line and rotational.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Concrete, Representational, Abstract (CRA)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Collaborative Learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -
Feedback
It has been shown that good feedback can make a significant difference to a student’s future performance.
Go to resource -
Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Practical numbers: Part 1
In this lesson, students explore standardised measuring systems.
Go to resource -
Syllabus BITES
Syllabus BITES contains a series of modules that introduce transformations in the Cartesian plane. Each module focuses on a different transformation – translation, rotation, reflection and combinations.
Go to resource -
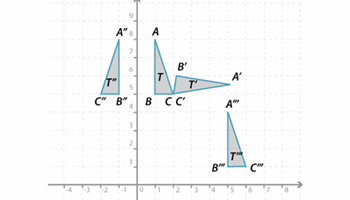
Transformations of the plane
This resource, focusing on transformations of the plane, gives detailed explanations for teachers and students of the curriculum content, worked examples and assessment questions.
Go to resource -
Transformations and congruence
In this unit, students learn to understand and use the terms ‘reflection’, ‘rotation’ and ‘translation’, recognising what determines each type of transformation.
Go to resource -
Rotations in the Cartesian plane
An interactive tool to investigate anticlockwise rotations of a triangle in the Cartesian plane.
Go to resource -
Transformations
This resource allows students to see the effect of different types of transformations on a triangle on a Cartesian plane.
Go to resource -
Transformations – rotation
This resource allows students to see the effect of rotation on a triangle on a Cartesian plane. You can adjust the position of the centre of rotation.
Go to resource
