Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M7N05
Numeracy Progression: Number and place value: P9
At this level, students will round decimals to a specified number of decimal places and connect the process of rounding up or down to prior experiences in rounding (for instance, 289 to 300). They know that rounding is a quick way of estimating an answer in an expression or problem (such as rounding $1454.85 to $1500) and that rounding simplifies unnecessarily complicated arithmetic calculations. For example, when we need to buy 28 items that cost $4.70 each, we can estimate the cost as 30 × 5.
Students will understand the appropriateness of rounding and its purpose. For example, is the purpose to round to a certain accuracy or a specified number of places (for a science experiment or a carpet estimate) or is the task to find a rough idea (a quantity of soil for the garden)?
Additionally, students can use rounding to check the actual answer to certain problems. Were they close? Did they work through the problem correctly? Was their estimate fit for purpose for the context? Asking questions is a useful approach for teaching rounding.
Students need to have a strong sense of place value, especially of decimal numbers. They need to understand that the purpose of rounding numbers is to establish which whole number the number in question is closest to, given the context. Knowing the intervals between two integers and a given rational number is required. The rule of 5 will need to be revised: 5 or more rounds up, less than 5 rounds down.
Linear Arithmetic Blocks (LAB) are a useful tool to help students understand rounding as a process of establishing which number is closest. They are a simple model for decimal numbers. Students can compare numbers, as well as demonstrate arithmetic operations using LAB. Use manipulatives such as multi-base arithmetic blocks (MAB) and representations such as factor trees. Use a variety of real-world examples, such as buying paint for your bedroom wall. For example, a wall is 2.7 m × 2.4 m, and a tin of paint covers
3.8 m2. How much paint is needed?
Students should understand and be comfortable using the following terms and notations:
- whole number, decimal number, rational number
- product
- rounding
- place value
- leading digit.
Teaching and learning summary:
- Revise the rule of five: 5 or more rounds up and less than 5 rounds down.
- Extend students’ knowledge of place value to rounding of decimals, including techniques such as rounding to the leading digit.
- Show students how to check that the accuracy or rounding is suitable for context and purpose.
- Model rounding to the nearest tenth, hundredth and thousandth, as well as tens, hundreds, thousands.
- Use estimation strategies to simplify real-world calculations.

Students:
- understand that numbers can be represented in a variety of formats
- understand the term ‘rounding’
- round a decimal to a given number of decimal places and whole numbers to an approximate number of places
- round and estimate to check the reasonableness of solutions
- use concrete, pictorial representations and abstract algorithms to show rounding
- round to the nearest tenth, hundredth, thousandth, as well as tens, hundreds, thousands.
Some students may:
- misplace the decimal point when adding or subtracting two decimal numbers or lose a zero when rounding larger numbers.
- not always make the connection between the digits and the size of the numbers.
- not realise that if the decimal needs to be rounded up that all decimal places are rounded up.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- I am learning to understand the conventions of rounding.
- I will use rounding to estimate the results of calculations with whole numbers and decimals.
Why are we learning about this?
Even though it would be far more satisfying, the numbers we encounter daily are often not nice round numbers. Flip through any catalogue that might be lying around. Making calculations with numbers like 4.25 or 289 is more time-consuming and has a higher likelihood of error than with numbers like 5 or 300. Adjusting numbers thoughtfully won’t change the result greatly, but it can significantly simplify the processing.
What to do
Grab a dice and a deck of cards and find a partner to play against. This is a great opportunity to impress your folks. Here are the rules of a simple rounding game:
- Remove the jokers and all face cards from the pack of cards. Aces can stay and count as 1 in this game.
- Player 1 rolls the dice.
- Player 1 draws six cards from the top of the deck.
- Both players write down the numbers shown on the cards in order. If I drew 7, 8, 5, 1, 10 and 4, then I would write down 7851104.
- Counting from left to right, place a decimal point after the number shown on the dice. If the dice shows 3, my number would be 785.1104.
- Repeat for Player 2.
- Once both numbers have been written down, it’s a race to see who can add them first (or subtract, multiply or divide, depending on the level of challenge you fancy).
- But there’s a catch. You don’t have to add the exact two numbers you see. To be fast, both players are allowed to round the numbers and estimate the sum. My number could be quickly rounded to 800. Fastest calculator wins. Verify with a digital calculator.
- Each round you draw one less card and ignore one number on the dice. So, the second round you will draw five cards and ignore the 6 on the dice. The third round you draw four cards and ignore the 5 and 6 on the dice.
Success criteria
- I can use my knowledge of place value to round numbers to a given number of decimal places.
- I can use estimation to simplify calculations while still achieving accurate results.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Estimating and rounding decimals
In this lesson, students draw on prior knowledge of rounding whole numbers.
Go to resource -
Round decimals to a specified number of decimal places
This informative page is an access point to misconceptions, interactive teaching resources and teaching ideas on this topic.
Go to resource -

Multi-base Arithmetic Blocks (MAB)
This resource explains what MABs are and how to use them in the classroom.
Go to resource -

Decimals: meaning and models – the part-whole relationship
Find one way to model and give meaning to decimal numbers.
Go to resource -
Properties of number
This resource focuses on factors, multiples and prime factors. It also looks at how to apply these principles when using fractions. There is an informative video on how to present this material to students and the common misconceptions they may hold.
Go to resource -
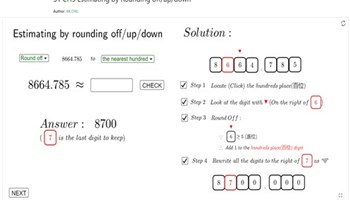
Estimating rounding off/up/down
Students can practise rounding up and down to the nearest hundred, ten, integer, first decimal place or second decimal place.
Go to resource -
Round the Dice Decimals
This activity allows for students to practise rounding decimal numbers to the nearest whole number. It encourages students to record their results, notice patterns and make predictions.
Go to resource
Assessment
By the end of Year 7, students round decimals to a given accuracy in relation to the appropriate context. Students also use rounding and estimation to check the reasonableness of their solutions to problems.
-

Translating between repeating decimals and fractions
In this resource, students convert between repeating decimals and fractions. There are teacher notes and ideas on how to spot and address different misconceptions the students may hold.
Go to resource -

Decimals, rounding and truncations
This interactive allows students to repetitively practise rounding and compare the same number to multiple decimal places.
Go to resource