Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M6M02
Numeracy Progression: Understanding units of measurement: P8
At this level, students refine their understanding of area and perimeter and establish the formula for the area of a rectangle and use it to solve practical problems.
Ideally, enable students to discover the area formula themselves through practical investigation. When measuring the area of familiar shapes such as a rectangle, students will use square centimetres or grid paper to cover regions, and they may discover familiar representations (such as rows and columns that resemble arrays used in multiplication). From here, they can be supported to generalise a rule for area of rectangles: A = L × W.
Provide practical activities in which students will further their understanding of the fact that area and perimeter are not dependent on each other (for example, shapes with a perimeter equal to 12 cm may vary in area, depending on their dimensions).
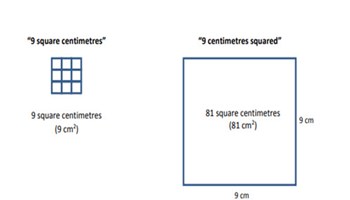
Use explicit teaching and questioning to extend students’ understanding of relevant units used to measure area, moving from measuring with squares to cm2.
Provide students with problems to solve involving the comparison of lengths and areas. Area is a two-dimensional quantity linked to covering regions using standard units such as cm2 and m2 and links to multiplicative thinking.
Perimeter is the one-dimensional measure around a shape. It relates to measuring the boundary or distance around a closed figure, and links to additive thinking.
Teaching and learning summary:
- Provide practical activities to investigate perimeter and area.
- Explicitly teach and model how to measure area using formal units.

Students:
- use examples to explain how to measure area and perimeter of rectangular shapes
- use the area formula to calculate the area of rectangular shapes
- explain how to find the area of a figure that is composed of other shapes
- use reasoning strategies to find the area of rectangular shapes.
Some students may:
- be developing their understanding of the conservation of area. They may experience difficulty understanding that if a shape is cut up and reformed it will still have the same area (e.g. a trapezium can be made into a rectangle). Use paper folding, where students divide and cut a rectangle into two identical triangles to form a parallelogram or an isosceles triangle. Through recognising that the area does not change after the shape has been transformed, students may better understand the principle of conservation of area.
- lack the spatial awareness to break a shape into separate parts, determine the area of each, and then put back together to give total area for the original shape. Developing spatial awareness and an understanding of the properties of shapes will also help students comprehend the relationship between area and perimeter.
- not fully understand area and perimeter. Use a variety of activities to demonstrate the lack of relationship between the one-dimensional perimeter and the two-dimensional area. Students may believe that surfaces with the same area must have the same perimeter, and vice versa. Using grid paper or geoboards will help students identify that these attributes are separate. Students can create different rectangles with an area of 16 cm2 then calculate the respective perimeters. This can lead students to make conclusions about their findings as they describe the characteristics of the rectangles.
- confuse formulas for area and perimeter and have difficulty determining which formula to use when measuring both attributes. This can happen if the concepts for area and perimeter are introduced simultaneously or by teaching the abstract formulas too quickly without providing students adequate time to comprehend their meanings. Use targeted teaching strategies to enable students to discover the formula themselves through recording dimensions and area in a table and look for patterns.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how to measure area using formal units.
- We are learning how to decompose and rearrange shapes to find their areas.
Why are we learning about this?
- Area helps you to quantify physical space. In real life, area measurements can help with working out quantities, for example, how much wallpaper is needed to cover a wall.
What to do
- Find a large box. Estimate how much wrapping paper you would need to wrap the box. Record your estimation.
- Cover one face of the box with a sheet of wrapping paper. Mark the around edges of the box on the non-coloured side of the wrapping paper. Work out the area of that face. Record your answer.
- Repeat the steps above for the remaining five faces of the box.
- Calculate the total area of the wrapping paper needed to cover the box. Draw a diagram to show all your measurements.
Success criteria
I can:
- find the area of a rectangular shape
- combine areas of a shape when working out the area of a box
- estimate and work out how much wrapping paper is required to cover a box.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Culturally responsive pedagogies
Culturally responsive pedagogy is a form of teaching that incorporates learners’ cultural background and histories into classroom practice.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Farm fence fractions
In this lesson, we explore fractions, decimals and perimeter.
Go to resource -
Teacher guide: Year 6 area and perimeter
A guide for teaching Year 6 students about area and perimeter.
Go to resource -
Finding the area of a rectangle
Students use the area formula for rectangles to solve real-world and mathematical problems.
Go to resource -
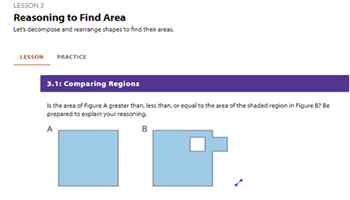
Reasoning to find area
This lesson shows how to decompose and rearrange shapes to find their areas.
Go to resource -
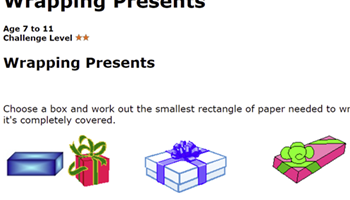
Wrapping presents
This problem provides a context to explore surface area and nets.
Go to resource -
Fencing the yard
In this task, students review and calculate perimeters and areas of rectangles and solve problems involving the comparison of lengths and areas, using appropriate units.
Go to resource -

Area and perimeter: Video and teaching guide
Use this video to explore concepts of area and perimeter, and connect these ideas to real-world situations.
Go to resource
Assessment
By the end of Year 6, students are using the formula for the area of a rectangle and angle properties to solve problems.
-
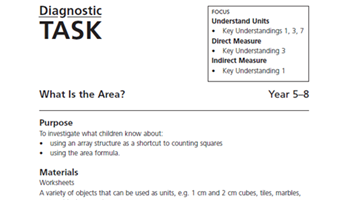
What is the area?
Use this diagnostic task to assess what students know about area and using the area formula.
Go to resource -
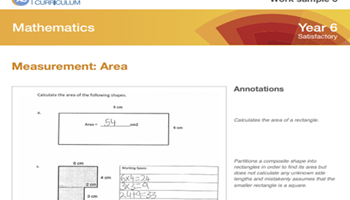
Mathematics: ACARA work sample portfolio summary – Year 6
Refer to ACARA work sample 6, 'Measurement – Area', and the related task for guidance in assessing students’ understanding of perimeter and area.
Go to resource