Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M2A01
Numeracy Progression: Number patterns and algebraic thinking: P3, Additive strategies: P7
At this level, students continue to appreciate and observe how patterns are present throughout mathematics. They recognise, describe and create additive patterns that grow or shrink by a constant amount. They also identify missing elements in pattern sequences.
Use visual patterns to consolidate student understandings of ‘growing patterns’ and ‘shrinking patterns’. Provide opportunities to create additive pattern sequences with physical materials such as counters, matchsticks, geometric shapes and blocks.
Model and encourage succinct summaries of what is happening in each pattern, for example, ‘Start with one square counter and add one square to each side, so each time add four squares altogether.’ Support students to make observations and use what is known to identify the missing element in a pattern sequence.
Observe and represent additive patterns in the world around them. For example, consider additive patterns of body parts in the class: How many legs on one person, two people, three people …? How many fingers …? How many heads …? Provide opportunities for students to record results as diagrams and in tables.
Follow a similar procedure for shrinking patterns starting with a large collection which is reduced in number by a constant amount.
Include a focus on the presence of patterns in cultural artworks, craft, dance, music and songs.
Teaching and learning summary:
- Explore the additive nature of patterns using physical and virtual materials, drawings, number charts and sequences.
- Foster curiosity about patterns and help students see them reflected in everyday life.
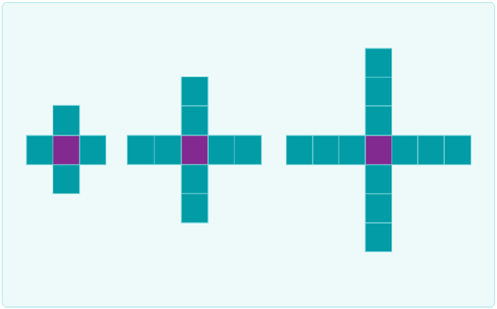
Students:
- recognise, describe and create growing patterns: additive patterns that increase by a constant amount
- recognise, describe and create shrinking patterns: additive patterns that decrease by a constant amount
- use what is known to identify the missing element in an additive pattern sequence
- record additive patterns using diagrams and tables.
Some students may:
- not yet grasp that skip-counting patterns are additive patterns. They may be able to skip-count fluently by two, five or ten starting from zero, but are unable to start from a multiple of the number without dropping back to zero, for example, when asked to count by fives starting from 15, they begin from zero.
- have trouble bridging across barriers such as 100 when skip-counting, for example, when asked to count backwards from 120 by tens, some students say: 120, 110, 190, 180, 170 … or they may omit 100, saying 120, 110, 90, 80 … 10. To address this, provide regular opportunities for students to count or skip count in different ways – oral counting, skip-counting physical objects, and written records of skip-counting.
- not yet skip-count from a non-multiple of the number. For example, when asked to start at 13 and count by twos students will say ‘I can’t’ or slip into a familiar sequence. For example, students might say ‘13, 15, 17, 19, 20, 22 …’ The 2, 4, 6, 8 pattern of the even numbers is much more familiar than the odd numbers. To address this, ensure first that students are confident counting to and from any multiple of the number before moving onto non-multiple starting points. Provide repeated opportunities to explore sequences on hundred charts and for oral counting with the various patterns.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are exploring growing and shrinking patterns.
Why are we learning about this?
- Patterns are at the heart of mathematics. Understanding patterns supports other mathematical understandings.
What to do
- Notice and enjoy patterns found in stories, poetry and songs. Listen to and/or create songs with growing number patterns, including skip-counting.
- Notice and discuss growing patterns in the world around you, for example, consider growing patterns involved when looking at a line of cars. How many wheels on one car, two cars, three cars?
- Practise skip-counting from different starting points and describe the rule, for example, 2, 5, 8, 11, 14 … ‘Start at two and add three each time’.
- Identify and explain visual patterns on clothing, wrapping paper, buildings, crockery, cards and furniture. Create a scrapbook to refer back to for ideas during arts and crafts.
Success criteria
I can:
- recognise, continue and create growing patterns with physical materials, for example, two leaves, four leaves, six leaves …
- identify the rule that creates a growing pattern, such as in the pattern 10, 12, 14, 16 … start at 10 and add 2 each time, then continue the pattern until a given number
- identify the rule that creates a shrinking pattern, for example, in the pattern 95, 85, 75 … start at 75 and subtract 10 each time, then continue the pattern until a given number
- identify the missing element in a pattern sequence, for example, 15, 20, ? , 30.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Culturally responsive pedagogy
Mathematics is not an exclusive western construct. Therefore, it is important to acknowledge and demonstrate the mathematics to be found in all cultures.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Recording additive patterns
Use this lesson to explore additive patterns, discuss them, and record observations in a table to identify patterns more easily.
Go to resource -

Skip-counting on the Number Line
Use this task to build familiarity with number lines by exploring skip-counting and common multiples.
Go to resource -

The Three Pigs
Use this resource to explore patterns that are emerging, and pose questions about the continuation of the patterns.
Go to resource -

The animals went in two by two
Use these activities to explore growing number patterns that decrease by twos, threes, fives and tens from any starting point.
Go to resource -
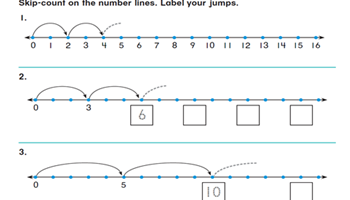
Skip-Counting and Equivalent Sets
Use these worksheets for students to identify and record skip-counting patterns.
Go to resource -

Exploring Rules and Patterns
Use these worksheets for students to identify missing numbers when using rule machines.
Go to resource -

Patterns
Use these activities to recall and use skip-counting by fives and tens to count collections.
Go to resource -
reSolve: Algebra: Equivalence
Explore equivalence by using weighted blocks to balance numbers on the scale.
Go to resource -

Let’s explore patterns
Use these videos to explore patterns and how students might think about them.
Go to resource

