Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M10A05
Numeracy Progression: n/a
At this level, students work with a variety of functions and relations and their rules, tables of values and graphs using digital tools. Students manipulate, explore, investigate, make conjectures and identify emerging patterns from functions and relations. This includes finding when two functions have the same value and when the values of a function lie within a given range, generating a sequence of results when a process is applied repeatedly, and transforming the graphs of a unit circle.
Have students work systematically with digital tools and algorithms to locate points of intersection between the graphs of two functions, which may be linear, quadratic or exponential between a linear function and a quadratic function or between a linear function and a circle.
Locate approximate values for the x-intercepts of quadratic functions with irrational roots, such as ƒ(x) = 3x2 – 4x – 6, by applying a bisection method and by zooming in iteratively using digital tools.
Teaching and learning summary:
- Revise and consolidate learning on linear, quadratic and exponential functions and related algebra, tables of values, number patterns and graphs.
- Develop confidence in relating coordinates of points on the Cartesian plane to tables of values, rules of functions and relations, and their graphs and transformations of these.
- Students solve problems involving locating axis intercepts, points of intersection, finding when the values of a function lie in a given range applying transformations, and implementing algorithms.
- Students find progressively refined approximations of intercepts and points of intersection between two functions by applying a bisection algorithm and by zooming in iteratively using digital tools.
Students:
- use digital tools to manipulate, explore, investigate, make conjectures and identify emerging patterns from functions and relations, for example, transformations of the graph of the unit circle
- explore linear, quadratic and exponential functions and related algebra, tables of values, number patterns and graphs involving non-integer roots
- use digital tools to zoom in on and progressively refine approximations of points of intersection between two functions
- apply a bisection method to locate approximate values for the x-intercepts of quadratic functions with irrational roots, such as
f(x) = 3x2 – 4x – 6.
Some students may:
- not realise that irrational numbers are infinite when expressed as decimal numbers and hence are only represented by an approximation of their exact value.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to use the zoom-in functionality of graphing software to find the approximate location of points of intersection of two graphs.
Why are we learning about this?
Many practical problems involve solving equations that do not have exact solutions, or where the process of finding the exact solution is complicated and an approximation is sufficient. For example, many calculators and graphing software use algorithms to calculate approximate answers of irrational numbers when expressed as a decimal.
What to do
Intersecting graphs
Use a graphing tool such as a graphics calculator or GeoGebra to complete the following.
- Graph the functions y = 2x and y = x2 on the same set of axes and find the coordinates of any points of intersection of the graphs.
- Graph the functions y = 2x and y = 2x on the same set of axes and find the coordinates of any points of intersection of the graphs.
- Graph the functions y = x2 and y = 2x on the same set of axes and explore their points of intersection:
- Find the coordinates of the two points of intersection that have positive integer x and y.
- Find another point of intersection that is between –1 and 0, and has a decimal y value between 0 and 1. Find approximate coordinates for this point correct to 1 decimal place.
- Use the graphing tool ‘zoom’ feature to increase the detail around the point of intersection (more intervals with smaller decimal differences) and show that the x value of the third intercept is between –0.80 and –0.75. Find approximate coordinates for this point, correct to 2 decimal places.
- Continue zooming in on the point of intersection until the graphs almost look like two straight lines crossing. Then find approximate coordinates for the point of intersection correct to 3 decimal places.
- Use this approach to find approximate coordinates for the points of intersection of the functions y = 3x and y = 3x, correct to 3 decimal places.
Success criteria
- I can find the approximate location of any points of intersection of the graphs of two functions and systematically refine these approximations using the zoom functionality of graphing software.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Comparing graphs
This teaching guide provides a lesson plan, exercise, practice and answer questions, and advice on investigating functions, including finding the intersection of two graphs. The emphasis is on making sense and meaning from a mathematical investigation approach.
Go to resource -

Graphing calculator
This is a quick link to GeoGebra’s graphing calculator for students to use and experiment with.
Go to resource -
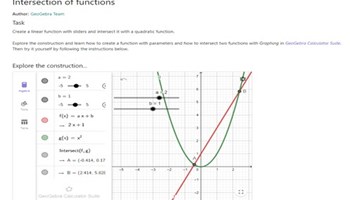
Intersection of functions
This interactive allows students to investigate the intersection and find coordinates between linear and quadratic functions.
Go to resource -

Table of values
This interactive provides the opportunity to find the (x, y) coordinates from two exponential functions. Encourage students to manipulate parameters to make meaningful connections.
Go to resource -

The bisection method
A detailed explanation of the bisection method and the bisection algorithm.
Go to resource
Assessment
By the end of Year 10, students can make and test conjectures involving functions and relations using digital tools.
-

Comparing graphs
This teaching guide provides a lesson plan, exercise, practice and answer questions, and advice on investigating functions, including finding the intersection of two graphs. The emphasis is on making sense and meaning from a mathematical investigation approach.
Go to resource -
Charlie's delightful machine
This activity involves using a systematic approach to determine the rules that determine when each of the four lights will turn on or off.
Go to resource