Year level: 4

Strand: Number, Algebra

Lesson length: 60 mins

In this second of three lessons, students use mathematical modelling to solve problems that involve financial decisions.

They will be guided to use the 4-step problem solving model to support them to unpack the problem, generate a plan to help solve it, and check their ability to work mathematically.

Students will explore different ways to estimate and form possible solutions to the total earnings over a period of time. The lesson allows students to be creative in the way they infer the stated problem and select strategies to find possible solutions.

They will communicate their thinking and justify their approach to the problem and their solutions.

Pocket money: Mathematical modelling Image

Achievement standard

Students use their proficiency with addition and multiplication facts to add and subtract, multiply and divide numbers efficiently. They use mathematical modelling to solve financial and other practical problems, formulating the problem using number sentences, solving the problem, choosing efficient strategies and interpreting results in terms of the situation.

Content descriptions

Students use mathematical modelling to solve practical problems involving additive and multiplicative situations including financial contexts; formulate the problems using number sentences and choose efficient calculation strategies, using digital tools where appropriate; interpret and communicate solutions in terms of the situation. AC9M4N08

Students develop efficient strategies and use appropriate digital tools for solving problems involving addition and subtraction, and multiplication and division where there is no remainder. AC9M4N06

Recall and demonstrate proficiency with multiplication facts up to 10 x 10 and related division facts; extend and apply facts to develop efficient mental strategies for computation with larger numbers without a calculator. AC9M4A02

General capabilities

Numeracy

Critical and Creative Thinking

  • Analysing (Interpret concepts and problems Inquiring)
  • Inquiring (Identify, Process and Evaluate information)

Students respond to one of the questions: Why is it important to know how to calculate multiple money amounts? How could you use this learning in your current lives? How might it be useful for you in future years?

Formative assessment

  • Observe the working out in students' workbooks while they are developing a plan or solving the problem and make notes on your observations.
  • Listen to students discussing their strategy choices with each other. Provide feedback on student’s strategies to support them to refine their ideas where necessary.
  • Be familiar with the concept of pocket money.
  • Estimation and approaches to make an estimate.
  • Share dollar amounts in different ways.
  • Follow steps to problem-solving and know problem-solving strategies they could use to find solutions.
  • Adopt a growth mindset and persist through a problem for which they do not have an immediate solution.

Some students may:

  • find it a challenge to read and understand the problem: there is choice in the way the money can be distributed if students elect to allocate a different value to the jobs performed. (The problem doesn’t state that the jobs are all of equal value)
  • require support to move their thinking from additive to multiplicative thinking when calculating costs for a four-week period (repeated addition to multiplication)
  • require support to shift their thinking when using estimation from wanting to calculate an exact value to using strategies to estimate an approximate value
  • require support and encouragement to move from inefficient to efficient strategies.

What you need:

Learning goals

Learning intention

  • We are using mathematical modelling to solve problems involving money.

Success criteria

By the end of this lesson, students can:

  • use the 4-step problem solving method
  • use rounding to estimate the amount of money earned over a period of time
  • use efficient strategies to calculate the total cost of earnings over a period of time.

Why are we learning about this?

Working with money is an essential skill in life. From the beginning of primary school we learn that there is an exchange process when we want to buy something. We also learn about needs and wants. It is important to understand the importance of spending, sharing and saving. As we move into our teen and then adult years we experience handling our own money and make financial decisions based on our earnings and what we can afford.

Problem-solving is an essential skill for life. Having a consistent problem-solving approach can help guide you through a problem. The ability to demonstrate strong problem-solving skills can also be important in your career. 

Learning hook 5 mins

  • Download and use the teacher’s slides to accompany your teaching. You will find this in the ‘What you need’ section.

Slide showing three children explaining task. They have a total of $15 to decide how to share between them for completing their jobs around the home.

Slide 2

  • Project Slide 2 of the Pocket money: mathematical modelling presentation. Ask:
    • What do you notice? What are you wondering?
    • What connections can you make?
    • What do you think today’s task might be about?
  • Use Slide 3 to remind students of the different ways we can partition number into equal and unequal shares.
  • Discuss examples of where this type of partitioning may occur with money problems, for example, siblings sharing allocation of money for jobs.

Explore 35 mins

Introduction to problem solving approach

  • Share the learning intention and success criteria using Slide 3.
  • Explain that in the lesson today we are going to explore different ways to calculate money amounts earned over a period of time. Show the first Mathematical modelling slide (Slide 5). The process is based on University of Adelaide’s Problem solving approach using Mathematical modelling.

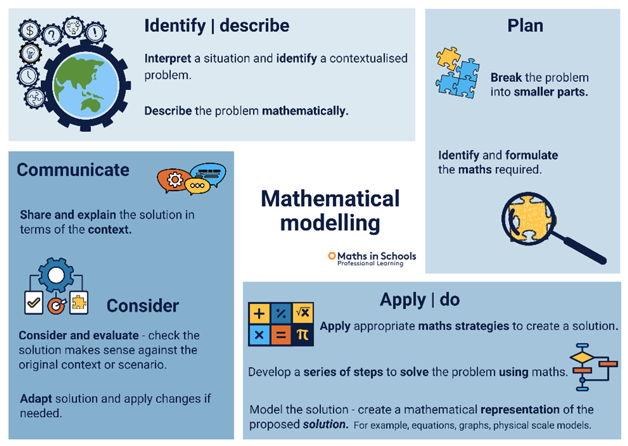
Slide showing mathematical modelling teaching approach, identify and describe, Plan, Communicate and Apply and do.

Slide 5

    • Explain that today we will be solving a maths problem related to pocket money. To help us, we will follow a 4-step method to guide our work and thinking. Introduce each of the steps to the students over the course of the lesson.
    • Slide 6: Present and Explain the Identify / describe stage of the process.
    • Slides 7-9: Present the problem to the students. Support the students to read and understand the problem. Unpack any unfamiliar vocabulary.
    • Slides 10 and 11: Present and explain the Plan stage of the process.
      • Present the problem-solving strategies to the students (Note: If students are not familiar with problem-solving strategies, present and define the strategies, including an example for them to follow).
      • Explain to the students that we can use problem-solving strategies to help us solve problems. Briefly share the list on the slide 7 and descriptions of the strategies to help students understand their role in solving problems.
      • Slide 12: Present and explain the Apply / do stage of the process.
      • Slide 13: Present and explain the Communicate stage of the process.
      • Slide 14: summarise the process and ask students to recall elements of the process. The slides include animation of the steps.

Practical component

      • Provide the worksheet: Pocket money. Ask them to read the problem carefully to understand what the problem is asking.
      • Allow students time to reflect on their options and make a choice based on their level of knowledge and understanding.
      • Invite students to develop a plan reflecting on the use of problem-solving strategies and mathematical strategies to suit the problem. Explain it is now time to put their plan into practice and use their mathematical skills to help find solutions to the problem.
      • Rove the classroom to check for understanding and provide questions to prompt students with mathematical thinking. Identify students to share their strategies with their peers during the ‘summarise’ stage. Encourage these students to practise how they will explain their thinking.

Remind students that they are to show all their working out in their workbooks. Encourage students to explore different strategies and find one that is efficient to use.

Summary and reflection 15 mins

  • Encourage the students identified earlier to share their strategies with their peers. Support students in their explanation with mathematical vocabulary and sequencing of steps. As students are sharing their thinking, record their strategy using materials/pictures and numbers (words) on an anchor chart. Acknowledge the student’s work with their initials.
  • Using a table and identifying patterns, begin to model how students could solve this same problem where each child receives an equal share each week.

Example: Amount earned over a number of weeks

  • We can calculate the total amount we could earn (or did earn) over a given time period. Let’s look at a four-week time period where the children earned the same amount each week.
  • If the children were given the same amount of pocket money to share ($12) and each received the same amount of money for doing the same jobs over the four-week period, how much money would they each earn?

Strategy 1: Repeated addition

We could add the amount for the four weeks: $3 + $3 + $3 + $3 = $12

However, if we were to then calculate the total amount earned over 10 weeks this would be time consuming. Let’s look at using multiplicative thinking.

Strategy 2: Multiplicative thinking

To calculate this amount, we can use a table to answer the question.

4 x $3 = $12

After four weeks they have saved $12.

How much would they save after 10 weeks? (Make explicit that the equation would be 10 x $3 = $30)

Differentiation (extension) 

Extending prompt: How much can we save over a six-month period?

Provide the problem of saving up for a big item. Explore earning and saving money over an extended duration, so they apply their additive or multiplicative thinking.

  • Use a table to work out the amount saved over 10 weeks, 20 or more weeks. What patterns do they notice?
  • Add these strategies to a chart as a reference for the students. Encourage students to use this resource as a guide as they continue to problem solve.
  • Invite students to revisit the problem and continue to explore options to find solutions.