Off the scale

Note: Download the teacher’s slides and resources to use with this lesson. Note that students will be working in groups and will only require one set of cards per group from the downloadable card sets.

Learning hook

• Divide the students into three groups. Assign each group one set of ten cards. If groups have less than 10 students remove cards so there are only enough for the number in the group. Have one student cut out the cards for their group.
• Use rope, string or lines of chalk (outside) to create three parallel timelines around 5m long, 1m apart.
• Explain that they have been given cards for different events in Australian history and need to place them on a timeline, based on when they think each event happened. Each timeline is for a different group: Australian science and nature, Aboriginal and Torres Strait Island Australians or Australian sporting events.
• Ask each student to hold their card and stand on the timeline at an appropriate place – on the right end is the event that occurred the longest ago and on the left is the most recent. Students try to space themselves based on when they think the various events occurred and discuss their timeline placement as a group.
• Use Questioning (or hints) to help students space themselves reasonably:
  • How long ago did the event on right-hand end occur?
  • How long ago would this point (halfway) be?
  • The timeline is about 5 m long – how many years would each metre on your timeline be?

One purpose of this activity is for students to use their time estimation, historical knowledge and reasoning skills. However, the actual correct placement of each event is not the main learning goal. It is rather for students to use proportional reasoning to place the events with roughly the correct order and spacing and to recognise the following:

• Most of the events for the Australian science and nature group and Aboriginal and Torres Strait Island Australians group are clustered quite close together at the left end (last few hundred years), with a few much more ancient events far more spread out. This makes it hard to differentiate the recent events as they are so close together.
• As all the Australian sporting events group have occurred in a much shorter space of time (160 years) they are more evenly spread.
• These examples show that linear scales are not always useful to highlight data trends, depending on the distribution of the data, thus providing the justification for consideration using a log scale.

The actual dates of the events are included in the final pages of the card sets and can be disclosed for students to check their reasoning. The teacher may also choose to discuss some of the locally or culturally significant events in more detail.

Constructing a log scale

Recap the main learnings from the introductory activity reinforcing that:

• if data is reasonably evenly distributed, a linear (normal) scale is appropriate, such as for the sporting events when each metre (or mark on a scale) could represent say 40 or 50 years
• when some of the data is very far apart from the other points (in orders of magnitude hundreds or thousands of times bigger), each metre (or mark on the scale) would need to represent 10,000 or 15,000 years which means all the smaller values (more recent events) almost sit on top of each other.

Explicit teaching

Go to slide 2 in the teacher’s slides and explain that to solve this problem, we’re going to use a log scale.

Use the Explain, Frame and Reframe approach to introduce why we use a log scale:

• Explain (teacher): If data is orders of magnitude apart and we want to understand the rate of increase we use a log scale.
• Frame (students finish statement): If data is orders of magnitude apart and we want to understand the rate of increase we use …
• Reframe (students answer): When do we use a log scale?
• Reframe (students answer): What does a log scale help us understand?

Ask the question: ‘What is a log scale and how do we make one?’ On a whiteboard draw two lines 1 m long, about 20 cm apart, and make a mark at each 10 cm to create a scale. Label the top scale Linear and label every other mark 0, 10, 20 … 50.

Use questioning to complete the scale to elicit the idea that the scale increases by the same number (5 or 10) in an additive way. Ask:

• What would this mark halfway between 0 and 10 be?
• What would in between 0 and 5?
• How is the scale increasing?

Explain that a linear scale is the ‘normal’ scale (like a number line) that we are used to seeing and using.

Label the second scale Log or Logarithmic. Label every other mark 1, 10, 100. Stop and ask:

• What do you think I should write by the one after the next mark?
• Can you explain how I am constructing this scale?
• What is different between this log scale and the linear scale?

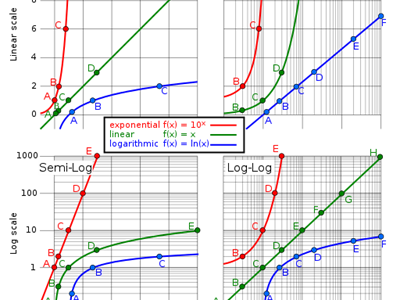
Key points to note are that a log scale:

• is multiplicative, so each increment represents multiplying by 10 not adding 10
• cannot start from zero.

Differentiation (extend): Advanced students may recognise logarithms as the inverse of the exponential function and understand that the value of a logarithm can never equal zero since there is no solution to the equation 10^x = 0.

Differentiation (support): For most students who have not been exposed to logarithms, a simpler explanation is to note that because  if the scale started at zero it would never increase, so instead it starts at 1. If smaller numbers are needed the scale could start at 0.1 or 0.01, but never 0.

Once the scale is complete, ask ‘How could we write this scale using index notation?’ or ‘How could we write this scale using powers of 10?’ and fill in 10⁰, 10¹, 10² and more under the scale.

Use an Explain, Frame and Reframe approach to summarise the key differences between a log and linear scale:

• Explain (teacher): As we move to the next mark on a log scale, we don’t add 10 but multiply by 10.
• Frame (students complete): As we move to the next mark on a log scale, we don’t add 10 but …
• Reframe (students answer): How are the increases on a log scale different to a linear (normal) scale?
• Explain (teacher): A log scale starts from one not zero.
• Frame (students complete): A log scale starts from …
• Reframe (students answer): On what number does a log scale start?

Ask: ‘What should I write at this mark halfway between 1 and 10?’

Incorrect answers could include 5.5 (linear thinking) or 5 (if a student thinks you multiply by 5, being half of ten, to get the half-way point). Emphasise what is changing in the numbers already on the scale and highlight the powers of ten.

If a student suggests 10^0.5 say: ‘Let’s use our calculators to work out what that would be’. Find that 10^0.5 ≈ 3.2 and mark this on the scale. Ask, ‘If I create a new mark on the scale half-way between 10^0.5 and 10¹ and what power should that be?’ Again, use calculators to confirm that 10^0.7 ≈ 5.6  and mark this on the scale.

Point out that while this is accurate, it is not very helpful to have a scale marked with 1, 3.2, 5.6, 10 if we want to plot points. Instead explain that it would be really useful if we could find the different powers to put onto 10 to get values like 2, 3, 4, 5 … and note that this is what mathematicians have done in the creation of log graph paper.

Show the image of the log graph paper on slides 2 and 3 and explain how the scale operates. Note that technically this is semi-log paper as only half the axes are on a log scale: the vertical axis is a log scale, but the horizontal axis is linear.

Paired activity / review – COVID-19 cases

Explain that during COVID-19 was the first time that data using a log scale was very widely seen and talked about in the media. New case numbers were reported and monitored daily, by state and territory, national governments, and global bodies like the World Health Organization.

A log scale was often used, as some rapid increases were seen and there was a focus on the rate of increase to try and understand how quickly the disease was spreading and whether measures like masks, border closures and lockdowns were working. While epidemiologists who study patterns of disease regularly use log graphs, many members of the general public (and government) struggled to understand the log graphs presented.

This activity asks students to create their own log graph to try and understand the rate of increase using actual data from the time, but consolidated into months (to reduce the number of data points to a manageable total).

Organise students into pairs and distribute a copy of the log graph worksheet one between two. The dates chosen cover the period when daily case number data was being reported in Australia.

Explain the activity using slide 4:

• In your pair, you should have two sheets: log graph paper and the data file: New COVID-19 cases.
• Mark the vertical scale on your log paper starting at 1, multiplying by 10 for each darker line.
• On the horizontal axis mark Feb-20 for the first mark and a different month for each mark up to Aug-22.
• Choose a state or territory or Total (all Australia).
• Plot the new COVID-19 cases for that month for your state or territory.
• Join your points with a curved (freehand) line.
• Write a few sentences explaining what your data shows.

Monitor students’ progress, being mindful to check for scales starting at one, multiplicative increases on the vertical scale and students using log rather than linear thinking when plotting intermediate points. Ask for students to share some of their observations from their graphs.

Optional: Distribute the data spreadsheet Excel file and have students create a graph for their chosen state or territory using a digital tool, switching between a linear and log scale.

Present slide 5 and ask students ‘Which scale is best and why?’ Use more detailed prompts such as:

• ‘Which scale is easiest to understand?’ Possible answer: ‘The linear graph is easier to understand, because we are used to seeing scales like that and it goes up evenly.’
• ‘Which graph gives more helpful information about the first year of the pandemic?’ Possible answer: ‘It’s hard to see what is happening in the first year on the linear graph because the numbers are so small, so the log graph might be better.’
• ‘Which graph would be more likely to convince you that measures such as masks and vaccinations are a good idea?’ Possible answer: ‘On the log graph, the initial numbers appear bigger so that might make you more likely to support measures to stop the spread.’
• ‘How are the graphs different? How do they tell a different story?’ Possible answers: ‘On the log graph, it looks like numbers are pretty flat towards the end period, but on the linear graph they seem to be coming down so this is a bit inconsistent and confusing.’ ‘The log graph seems to show a generally steady increase, then flattening at the end, whereas the linear graph shows nothing for the first 1.5 years and then massive numbers.’
• ‘How might the different graphs be used?’ Possible answers: ‘Epidemiologists need to study the rate of increase so would definitely use a log graph, but perhaps they are too confusing for non-specialists to understand.’ ‘Data is always used for a specific purpose so you have to be careful what the person or body showing you the graph believes and wants you to believe as that could influence how they present the data.’

Note that current sources of public information on case numbers such as the World Health Organization’s Coronavirus Dashboard and the Australian not-for-profit covid19data have reverted to using a linear scale, probably because of a lack of understanding of log scales among the public.

Slide 6: explain that log scales are not just used for data relating to epidemics. When measuring something that increases by significant orders of magnitude, a log scale is used. Ask students if they can guess these log scales from these images: earthquakes (measured on the logarithmic Richter Scale); pH or the acidity / basicity of a chemical; the loudness of sound (measured on a log scale in decibels); measuring light exposure for photography.