Why lesson planning is important for student success

Antje and David Leigh-Lancaster, Leigh-Lancaster Consulting 

 

Introduction

Lesson sequences are a series of related lesson plans that connect the content descriptions and achievement standards of the strands with the proficiencies and the mathematical processes, aligning curriculum with pedagogy and assessment.

Lesson planning is a practical way to realise the aims of Australian Curriculum: Mathematics Version 9 and work toward successful outcomes for students of mathematics.

This article discusses: 

  • the importance of knowing the mathematics core concepts and ideas to be addressed in a lesson and how they relate to learning progressions in the curriculum 
  • how lesson planning enables the effective use of classroom time, facilitates the structure and flow of a lesson, and outlines pedagogical approaches and activities
  • the benefits of collaborative planning for teachers and the school learning environment.

How these three components relate to Mathematics lesson planning is illustrated in Figure 1. 

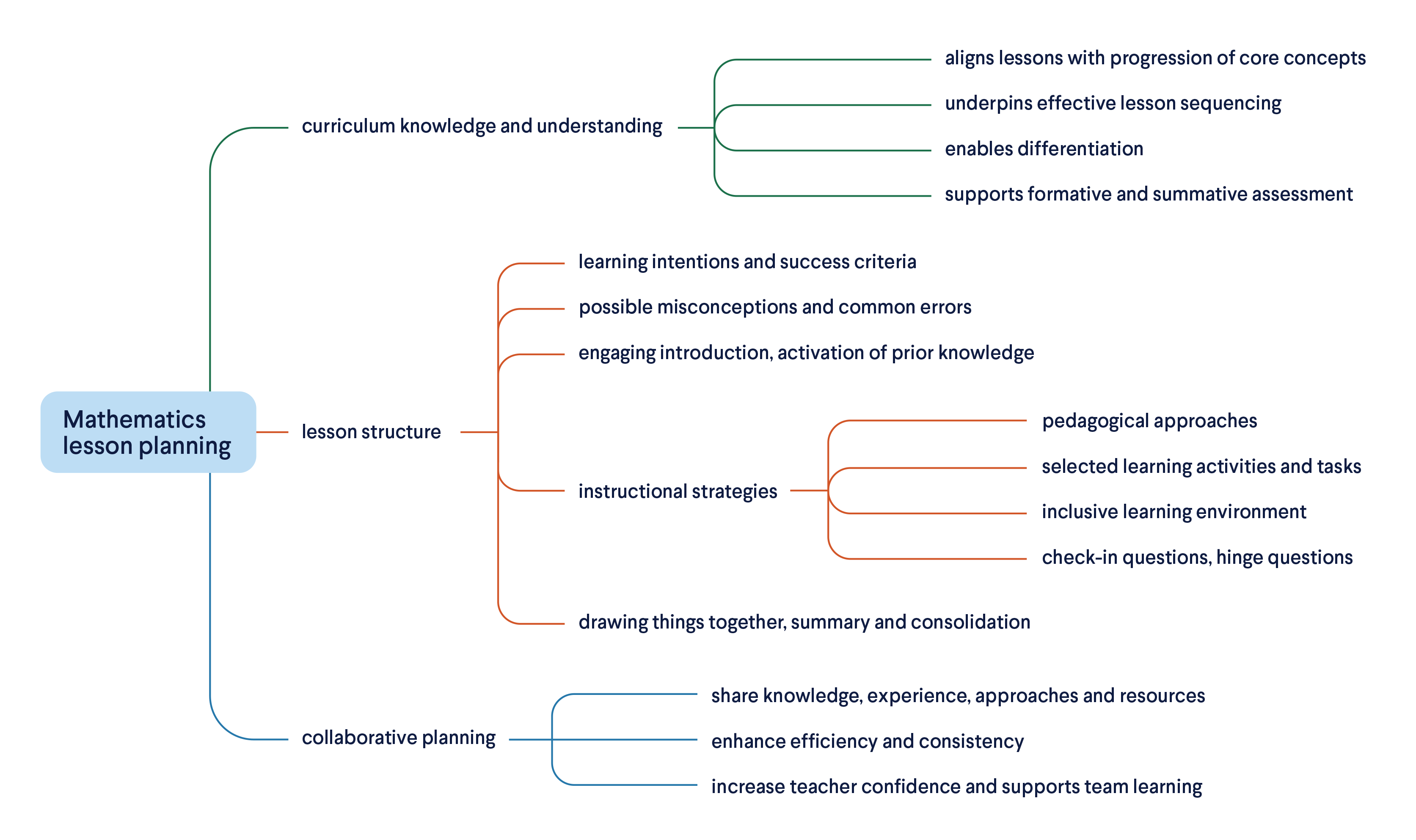
Diagram of a flowchart describing the three main components and various sub-elements of Mathematics lesson planning, sequenced from left to right.

Diagram of a flowchart describing the components of Mathematics lesson planning, sequenced from left to right. To the left, the flowchart starts with Mathematics lesson planning, which then flows to three main components: the first is Curriculum knowledge and understanding; the second is Lesson structure; and the third is Collaborative planning. The flowchart then flows to further elements of each component. Four elements flow from Curriculum knowledge and understanding: the first is Aligns lessons with progression of core concepts; the second is Underpins effective lesson sequencing; the third is Enables differentiation; and the fourth is Supports formative and summative assessment. The second main component of Mathematics lesson planning is Lesson structure, and this then flows to five further sub-elements: Learning intentions and success criteria; Possible misconceptions and common errors; Engaging introduction and activation of prior knowledge; Instructional strategies; and Drawing things together, summary and consolidation. The sub-element Instructional strategies flows to four further sub-elements: Pedagogical approaches; Selected learning activities and tasks; Inclusive learning environment; and Check-in questions, hinge questions. The final main component of Mathematics lesson planning is Collaborative planning, which flows to three sub-elements: Share knowledge, experience, approaches and resources; Enhance efficiency and consistency; and Increase teacher confidence and supports team learning.

Figure 1

Curriculum knowledge and understanding 

Familiarity with the curriculum is important for the following reasons. 

  • Understanding the broader progression of core concepts and ideas can help focus the lesson on the key mathematics learning that students are expected to engage with.  
  • It helps answer the questions, ‘How does this lesson fit within the learning progression for a given core concept?’ and ‘What has been covered previously and where does it lead to for other lessons within a specific learning sequence, and for related future learning sequences, including at other year levels?’ 
  • It enables teachers to identify where their students sit along the progression for the concept or idea being covered and helps answer the question, ‘How can I make this lesson inclusive of all learners in the class?’ 
  • Knowledge of the broader progression of core concepts and ideas underpins teacher capacity to check for understanding and ability to develop assessments along several steps of a learning prog

Lesson structure 

Good lesson planning considers the structure and flow of a lesson, ensuring that is follows a logical and coherent sequence that facilitates student understanding. It supports effective time management, and ensures the focus of the lesson is on the identified key mathematics. It also allows time to discuss and consolidate key learnings at the end of the lesson. 

Planning allows you to anticipate challenges and consider effective ways to address them, including pre-planning questions to check for understanding along the way. Working through tasks beforehand will help you see where students might struggle, identify any supporting resources they may need, and consider how the task can be differentiated, including developing effective enabling, extending and enriching prompts. 

Some questions to consider while planning a lesson. 

  • What mathematics understanding do I want students to engage with during this lesson, and how will I know if this learning has taken place? 
  • What prior knowledge will they need to access the intended learning? What proportion of my students are likely to have this background? 
  • What common errors and misconceptions might arise? What questions can I ask to help identify them? How will I support students to address them? 
  • What learning activities, tasks and pedagogical approaches are effective for building the desired mathematical thinking and understanding? 
  • Does the lesson provide opportunities for all learners to participate and experience success? 
  • For what proportion of the lesson will students be actively engaged in thinking, doing and discussing mathematics? 
  • How will I draw together, summarise and consolidate the important learnings of the lesson? 

Collaborative planning 

Collaborative lesson planning has several benefits, both for teachers and for the school learning environment. Some of the main benefits include the following. 

  • Collaborative planning efficiently draws on the collective experience and knowledge of the team, facilitates the sharing of practices and approaches, and fosters openness to new ideas and the confidence to try them out 
  • It promotes shared responsibility for student success.  
  • It enhances consistency and coherence in curriculum implementation within and across year levels, and provides students with a more connected learning journey. 

Lesson planning takes time and is an iterative process, so expect continual improvement from one implementation to the next. 

More lesson planning resources 

  • Planning tool:This resource provides a comprehensive set of lessons in topics by year level and strand mapped to the Australian Curriculum V9. It also identifies possible misconceptions and errors and includes supporting assessment tasks. 
  • Teaching strategy: Questioning This resource provides an overview of questioning in mathematics lessons and includes a video discussing the use of closed and open questions, and a video on transforming from closed questions to open questions.
  • Problem Solving: Opening up Problems article This article discusses how closed and open problems are related and details a specific example for the process of opening-up a closed problem.