Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
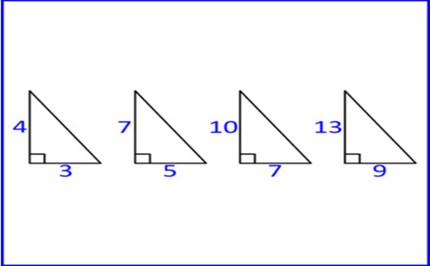
Right-angled triangles inquiry
This prompt will guide students to make a connection between Pythagoras and trigonometrical ratios. This can build the students' conceptual understanding of what a trigonometrical ratio is. The resource includes classroom examples, teacher notes and guided questions.
Additional details |
|
| Year level(s) | Year 8, Year 9 |
|---|---|
| Audience | Teacher |
| Purpose | Assessment task, Extension, Student task, Teaching resource |
| Format | Downloadable resources |
| Teaching strategies and pedagogical approaches | Collaborative learning, Differentiated teaching, Explicit teaching, Feedback, Mathematics investigation |
| Keywords | right-angled triangle, Pythagoras, trigonometry, ratio, similar, scale factor |
Curriculum alignment |
|
| Curriculum connections | Critical and creative thinking, Numeracy |
| Strand and focus | Measurement, Space, Build understanding, Apply understanding |
| Topics | Pythagoras and trigonometry |
| AC: Mathematics (V9.0) content descriptions |
AC9M8M06
Use Pythagoras' theorem to solve problems involving the side lengths of right-angled triangles
AC9M9SP02
Apply the enlargement transformation to shapes and objects using dynamic geometry software as appropriate; identify and explain aspects that remain the same and those that change |
| Numeracy progression |
Understanding units of measurement (P10)
Understanding geometric properties (P7) Multiplicative strategies (P9) Proportional thinking (P7) |
Copyright details |
|
| Organisation | Inquiry Maths |
| Copyright | © Andrew Blair 2012-21. Creative Commons BY-NC-SA 4.0. |
Related resources
-
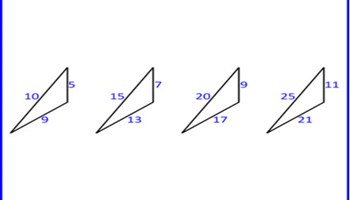
Scalene triangles
The prompt explores finding the angles in related scalene triangles.
Resource details -
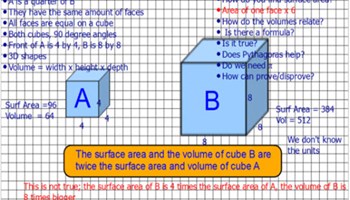
Volume ratios
Does doubling the side of a cube double the volume?
Resource details -
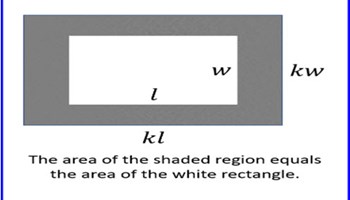
Equal areas
The process of calculating and comparing the areas of composite shapes, determining similarities and differences between the area, perimeter and height of shapes.
Resource details -

Inquiry maths
The Inquiry Maths website home page.
Resource details