Expected level of development
Australian Curriculum Mathematics V9: AC9M9M04
Numeracy Progression: Understanding units of measurement: P10, Proportional thinking: P6
At this level, students recognise that all measurements are estimates. Prior learning about place value and rounding comes to the fore as students consider the level of accuracy required in different contexts. Facilitate a class brainstorm to place a range of scenarios on a continuum that stretches from high to low requirements for accuracy. For example, compare the needs of NASA engineers designing spaceships to travel to Mars, to the drawing up a ‘four-square’ court in the schoolyard.
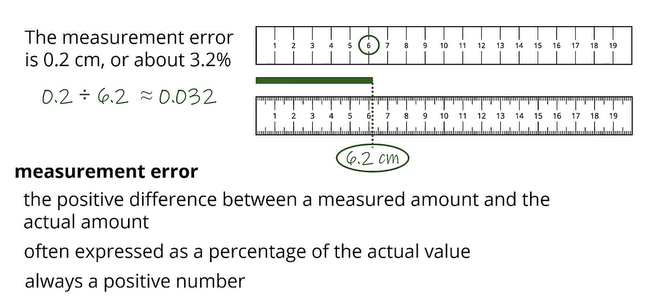
Provide opportunities for students to explore and describe the diminishing returns of adding additional places of accuracy and determine a suitable level of accuracy for everyday measuring activities. They should state the absolute error of a given measuring device and use this to calculate the relative error. Ensure students understand that the absolute error is the amount of error that could exist in a measurement. Put simply, it is the discrepancy between the actual value and the measured value.
This connection of understanding naturally leads to discussions on the accuracy of the measuring devices, so have students explore different contexts with different devices. Students should use the relative error to compare the accuracy of different measurements. Ask questions: would it be more accurate to measure your weight using a device with ± 0.1 kg absolute error or ± 1 Kg or 0.001 Kg, and in which contexts would different accuracies be acceptable?
Students should also be aware of the different possible sources of error, other than the inherent limitations of measuring devices, Introduce the concept of ‘calibration’ and that miscalibration of devices is common and can affect its measurements. Furthermore, there is always a level of random error that naturally occurs with any observations. Finally, an error may be the result of using a previously rounded measurement earlier in a calculation. It is important to explicitly demonstrate this for students as this may lead to significant errors in complex calculations across other subject areas, such as Science and Business and Economics.
Teaching and learning summary:
- Recognise that all measurements are estimates.
- Consider the level of accuracy required in a variety of contexts.
- Calculate the absolute and relative error.
- Compare the accuracy of different measurements using the percentage error.
- Discuss sources of errors.
- Consider impact of using a rounded measurement in repeated calculations.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -
Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
Percent error
Students are exposed to situations involving percent error, use the language of percent error and practise multi-step problems involving percent error.
Go to resource -
Practice: percent error
A series of questions on percent error in everyday contexts.
Go to resource -
Area problem: percent error
A student interactive determining the area under a curve on a graph using estimations and any number of rectangles. Students can change variables to see the difference between the exact or absolute answer and the approximate or relative answer.
Go to resource -
Solve problems involving percentages
A teacher resource to provide insight into students’ familiarity and misconceptions on problems using percentages, including percentage error. This resource gives further teaching ideas and teaching activities.
Go to resource
