Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M8N05
Numeracy Progression: Proportional thinking: P6, Understanding money: P8
At this level, students will use their knowledge and use the mathematical-modelling process to solve problems with rational numbers. They will apply efficient strategies and use digital tools, such as a calculator, where appropriate and verify solutions to various problems.
A wide range of contexts, extended problems and collaborative tasks will provide a platform to practise these skills, particularly in financial contexts. Engage students in everyday mathematics, considering scenarios like buying a first car, renting a room in a share house, budgeting and tax. Promote agency by surveying them on questions they have about money and finance. Encourage students to use and apply the correct mathematical terms and vocabulary for these real-world problems. Students should evaluate how realistic their models are. For example, if they are creating a personal budget, have they included all the elements that would be present in an adult's household budget?
Students use percentages in financial contexts to solve problems involving percentage increase and decrease, finding the percentage profit or loss and calculating percentage discounts and mark-ups. Students build on this knowledge to use multipliers above one to increase an amount by a given percentage. It is important to discuss and model situations involving similarities and differences between percentage increases and decreases.
Teaching and learning summary:
- Use financial contexts and the mathematical-modelling process to formulate problem statements and solve problems.
- Introduce a range of financial vocabulary and discuss issues or concerns that interest students in this topic.
- Revise using number knowledge and skills to solve practical problems in a range of contexts.
- Revise previous knowledge of percentages – expressing two quantities as a percentage and calculating the percentage of an amount.
- Discuss different ways of representing numbers, for example, with the symbol %, as a fraction, and as a decimal.
- Demonstrate how to find a percentage increase or decrease.

Students:
- find appropriate and efficient approaches when solving practical problems
- are confident with percentages and can express a percentage in different forms
- understand a range of simple financial terms and instruments
- choose and solve problems appropriately and efficiently, as well as communicate and justify their choices.
Students may:
- be uncomfortable with non-natural rational numbers.
- have had little exposure to the contexts explored in examples and need some accompanying vocabulary or explanation.
- be unfamiliar with the idea of a percentage greater than 100%.
The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning to model personal income variation across Australia.
- We use the tax tables to calculate personal income tax.
Why are we learning about this?
According to Benjamin Franklin, ‘death and taxes’ are the only two certainties of life. Tax is an important part of our lives. It pays for the roads we drive on, the school and doctor you attend, and even this website you are using. Society couldn’t function without taxes. Think ahead to when you are earning a salary. Ask yourself how much tax you will have to pay. Think about how much of your salary you will have left to budget and plan for the future in a realistic way. Here’s how it works.
What to do
The Australian Bureau of Statistics has compiled data on the mean and median salaries in an array of localities around Australia.
- Scroll down to the heading that says Data downloads and select Table 2.
- Each tab on the spreadsheet (at the bottom of the page) provides different granularity of data. Look through them to find places of interest to you. It could be where you were born, somewhere you’ve been on holiday, or a place you dream of living one day.
- Write down the median salary of these places. (Those of you who have studied the statistics topic will already know why we’ve chosen the median!)
- These salary figures are not an accurate indication of how much you might receive in your bank account each week or fortnight. The personal income tax you need to pay must be subtracted first. Why do you think salaries are quoted in this way? Why wouldn’t the after-tax figures be shown? I’ll leave that question to you. Maybe it can spark a conversation at your dinner table.
- Using this link, you can find the table: Resident tax rates 2022–23. By hand, calculate the after-tax salary for each of the locations on your list.
- Once you have completed your calculations, verify that you are correct by using one of the many pay calculators online.
- Do you notice any differences in the gaps between the before-tax and after-tax figures? Are they closer together or further apart?
- What does that tell you about the Australian taxation system?
Challenge
You have compared salaries by location but another interesting method for comparison is by industry.
- Find some data online on the ABS site that approximates the median salary for different industries in Australia and repeat the process from above.
- Do you have any idea which industry you might like to work in one day?
- Maybe you could use the after-tax salary you’ve calculated as the basis for a weekly personal budget for your future.
- Of course, it’s extremely difficult to predict the future, so your budget is likely to have errors. Can you think of what some of these might be?
Success criteria
- I can use the tax rates to calculate personal income tax for a range of salaries.
- I can model personal income for a range of different Australians.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Explicit teaching
Explicit teaching is about making the learning intentions and success criteria clear, with the teacher using examples and working though problems, setting relevant learning tasks and checking student understanding and providing feedback.
Go to resource -

Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Shooting 3-pointers: Part 1
In this lesson students are guided through solving a problem using mathematical modelling.
Go to resource -

Shooting 3-pointers: Part 2
In this lesson, students conduct a statistical investigation.
Go to resource -
Solving problems with percentages
In this resource, students are presented with a series of problems with the solutions fully explained. There are similar problems for the students to try.
Go to resource -
Increasing and decreasing quantities by a percentage
Students use a modelling exercise to practise converting, recognising and representing percentages, decimals and fractions.
Go to resource -

Money and financial mathematics
In this resource, teachers are taught to use questioning to guide students to successfully solve problems involving profit and loss.
Go to resource -

Teacher and student guide to mathematical modelling
This guide trains teachers to think and teach with a mathematical modelling mindset. Students use their investigative skills to solve real-world problems.
Go to resource -

Electric vs Petrol Cars
In this task students develop reasoning by analysing the costs of an electric vs petrol powered vehicle.
Go to resource
Assessment
By the end of Year 8, students use mathematical modelling to solve practical problems that involve ratios, percentages and rates in measurement and financial contexts.
-

Profit and loss
Students answer a series of questions based on scenarios where two shop owners have made both a profit and loss. They are required to calculate profit amount, compare profits and calculate the percentage profit.
Go to resource -
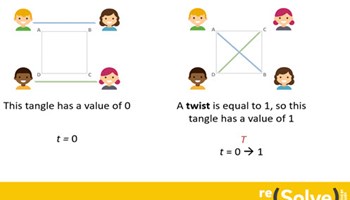
Rational tangles
This mathematics investigation prompts students to solve a ‘dancing’ problem with ropes using rational numbers. This task is for students who are are familiar with adding fractions.
Go to resource