Planning tool
Year levels
Strands
Expected level of development
Australian Curriculum Mathematics V9: AC9M3N03
Numeracy Progression: Additive strategies: P8, Number and place value: P5
At this level, students consolidate and deepen place value knowledge of two- and three-digit numbers. They do this by partitioning, rearranging and regrouping numbers to help in addition and subtraction calculations.
Use physical and virtual materials and visual representations to explore the proportional nature of place value parts when solving addition and subtraction problems. Provide repeated opportunities for students to explore different ways of partitioning, rearranging and regrouping when making calculations. For example: they explain that 163 + 28 can be more easily solved by breaking the numbers into place value parts, that 160 + 20 = 180 and 3 + 8 = 11, which then becomes 180 + 11 which makes 191.
Pose addition and subtraction problems horizontally (rather than vertically) to encourage students to think about problems in terms of place value parts. Ensure that students know they can rewrite and think about addition and subtraction problems horizontally, even if they are presented vertically to begin with. Use regular number talks to develop mental computation strategies. Include a focus on applying addition and subtraction strategies in a range of contexts, including through story problems.
Ensure students understand that different strategies will be more efficient at different times, for different people and across different problems.
Encourage students to value depth over speed. Celebrate sense-making, reasoning and lessons learned from mistakes when exploring and sharing strategies.
Teaching and learning summary:
- Use classroom talks and play-based explorations, in conjunction with explicit teaching, to support key understandings.
- Encourage reasoning, and emphasise the similarities and differences between different computation strategies used.

Students:
- justify choices when partitioning and regrouping numbers to perform addition and subtraction
- mentally solve addition and subtraction problems using partitioning, rearranging and regrouping, and explain the strategy used
- use written recordings to clearly display the solution used
- apply strategies involving partitioning, rearranging and regrouping when solving worded problems.
Some students may:
- be able to identify place value parts and count orally to 100 and beyond but still think about two- and/or three-digit collections additively in terms of ones (for example, understand 468 as the sum of 400 ones, 60 ones and 8 ones). To address this, consolidate place value understanding by comparing and ordering two-digit numbers (for example, which is larger – 2 bundles of ten and 3 ones, or the number 41 shown on a number line), counting forward and backward by tens and ones, and by renaming (for example, 32 is 3 tens and 2 ones; it’s also 32 ones; and it can also be 2 tens and 12 ones).
- consider each digit in an addition problem as a separate number as opposed to representing a place value part. When using the vertical or column method, failing to recognise the place value of the digits leads to a lack of reasoning and precision. To address this, present addition problems horizontally and create habits of reasoning that draw on place value understanding through number talks and other activities that focus on mental computation and breaking numbers up into their place value parts.

- subtract the smaller digit, regardless of which appears first when using the vertical or column method, indicating a lack of reasoning and understanding of the operation being used. To address this, present subtraction problems horizontally and create habits of reasoning through number talks and other activities that invite mental computation strategies and involve thinking in terms of place value parts.

The Learning from home activities are designed to be used flexibly by teachers, parents and carers, as well as the students themselves. They can be used in a number of ways including to consolidate and extend learning done at school or for home schooling.
Learning intention
- We are learning how place value parts help solve addition and subtraction problems.
Why are we learning about this?
- We use addition and subtraction in everyday contexts.
What to do
Use two- and three-digit numbers every day.
- Go on a number hunt. Look for, recognise and read the numbers around you, for example, numbers you notice around you on signs, calendars, speed signs and houses.
- Use everyday opportunities to practise using mental addition and subtraction strategies, such as predicting the change you will get at the store.
- Play ‘Guess my number’ or other games to put place value understanding into practice. Player 1 writes a two- or three-digit number on a piece of paper and the Player 2 asks ‘yes/no’ questions about it until they guess it. Example questions could be, ‘Is it larger than 500? Does it have an odd number in the hundreds place?’.
See mistakes as opportunities
- Know that mistakes are normal whenever we are learning or growing.
- When you get an incorrect answer, take the time to be curious about the mistake and see if you can learn from it. Which part of your strategy doesn’t quite make sense? How else could you approach the same problem?
Success criteria
I can:
- use the relationship between addition and subtraction to make some calculations
- solve addition problems mentally and verbally (for example, without pencil and paper) using place value parts
- solve subtraction problems mentally and verbally (without pencil and paper) using place value parts.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-

Concrete, Representational, Abstract (CRA model)
The CRA model is a three-phased approach where students move from concrete or virtual manipulatives, to making visual representations and on to using symbolic notation.
Go to resource -
Culturally responsive pedagogy
Mathematics is not an exclusive western construct. Therefore, it is important to acknowledge and demonstrate the mathematics to be found in all cultures.
Go to resource -

Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -

Questioning
A culture of questioning should be encouraged and students should be comfortable to ask for clarification when they do not understand.
Go to resource -
Multiple exposures
Providing students with multiple opportunities within different contexts to practise skills and apply concepts allows them to consolidate and deepen their understanding.
Go to resource -
Classroom talks
Classroom talks enable students to develop language, build mathematical thinking skills and create mathematical meaning through collaborative conversations.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-

Picture Storybooks: Year 3 place value
Use picture storybooks regularly to spark curiosity and interest in place value and related concepts.
Go to resource -
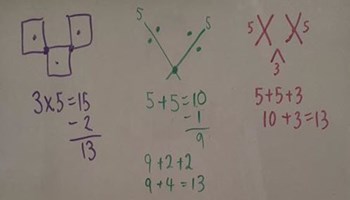
Classroom Talks: Year 3 – Place Value
Run 5- to 15-minute classroom talks regularly to consolidate and build upon the foundations of place value.
Go to resource -

resolve: Addition: Chess – The Rook
Explore addition using place value parts using the concept of chess.
Go to resource -
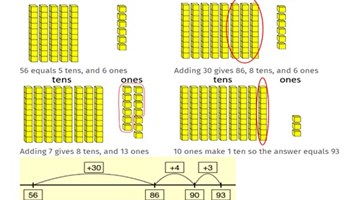
Addition and subtraction with whole numbers
Use this unit to explore situations involving addition and subtraction where students choose strategies, using place value understanding.
Go to resource -

Which would you do in your head?
Encourage students to think about which strategies suit them best when solving different addition and subtraction problems.
Go to resource -

Wishball challenge: hundreds
Encourage students to think about the best strategies to use when solving different addition and subtraction problems.
Go to resource -
Composition and calculation: 1,000 and four-digit numbers
Explore the composition of 1,000 and four-digit numbers.
Go to resource

