Expected level of development
Australian Curriculum Mathematics V9: AC9M10M05
Numeracy Progression: Proportional thinking: P7
At this level, students use a mathematical modelling approach in a range of contexts for problem-solving and modelling practical situations. These include drawing plans and elevations to scale, using ratio and proportion when making a prototype, and using estimation. Some of their enquiry may be investigated with hands-on materials and digital software programs.
Students are expected to be able to formulate questions to problems, identify and make comparisons between variables and elements to consider for a given context. Students brainstorm and consider a variety of approaches to find solutions efficiently and effectively. They must also be able to interpret their results and consider whether their model was successful. Refining and listening to feedback along the way is essential.
Importantly, students report and communicate their method, findings and conclusions, and identify limitations and those elements of their modelling that could be improved or refined.
Teaching and learning summary:
- Demonstrate how measurement with ratios, proportion and scaling is used in a range of real-world contexts taking a mathematical-modelling approach.
- Make use of measurement skills when problem-solving.
- Encourage students to brainstorm, use creativity and listen to feedback when creating and using mathematical modelling to solve problems.
- Give students opportunities to communicate their findings to the class or small groups, or as an assessment task.
Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
Teaching strategies
A collection of evidence-based teaching strategies applicable to this topic. Note we have not included an exhaustive list and acknowledge that some strategies such as differentiation apply to all topics. The selected teaching strategies are suggested as particularly relevant, however you may decide to include other strategies as well.
-
Worked examples
A worked example is not just a pre-worked question that is given to the students. There are several types of worked examples and ways of using them.
Go to resource -
Collaborative learning
For group work to be effective students need to be taught explicitly how to work together in different settings, such as pairs or larger groups, and they need to practise these skills.
Go to resource -
Mathematics investigation
By giving students meaningful problems to solve they are engaged and can apply their learning, thereby deepening their understanding.
Go to resource
Teaching resources
A range of resources to support you to build your student's understanding of these concepts, their skills and procedures. The resources incorporate a variety of teaching strategies.
-
A piece of cake
In this lesson, students build on their skills in finding volumes and surface areas of prisms and cylinders to design a multi-level celebration cake for a party.
Go to resource -
Mathematical modelling: a guidebook
An excellent guide for teachers to learn about and employ mathematical-modelling projects in the classroom. The guide discusses what mathematical modelling is, discusses a framework that students can follow, describes types of models and provides age-appropriate example problems.
Go to resource -
Teacher package: mathematical modelling
This site gives descriptions and approaches, and provides a number of links to real-world example problems to take inspiration from.
Go to resource -
Understanding compound interest
Students learn how compound interest works and why saving now can help you later.
Go to resource -
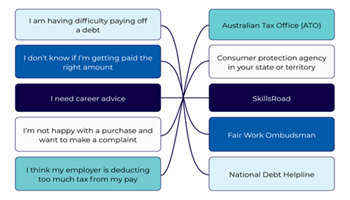
Different ways to pay
Students learn about the pros and cons of various payment options, what happens to their money, different consumer products and where to go for more information.
Go to resource
Assessment
By the end of Year 10, students can use mathematical modelling to solve practical problems involving proportion and scaling, evaluating and modifying models, and reporting assumptions, methods and findings.
-
Constructions
A modelling activity that uses geometry and scaling, and applies this knowledge to a real-world Defence problem.
Go to resource -
Mathematical modelling: a guidebook
An excellent guide for teachers to learn and employ mathematical modelling projects into the classroom. The guide discusses what mathematical modelling is, discusses a framework that students can follow, describes types of models and provides age-appropriate example problems.
Go to resource -
Seaside
This video employs knowledge of geometry, similar triangles, scale drawing and loci. An effective short activity to use on the board in the classroom.
Go to resource