Year level: 10

Strand: Space / Algebra

Lesson length: 55 mins

This is the second lesson in the Capital Airways series and follows the prior lesson Capital Airways: Part 1. Students investigate a network through an airline route map. The task is a mathematical modelling activity whereby students collaborate to re-design the network map to improve the airline’s profitability.

Capital Airways: Part 2 Image

Achievement standard

Students interpret networks used to represent practical situations and describe connectedness and use mathematical modelling to solve problems in financial and other applied situations, applying linear functions as appropriate.

Content descriptions

  • Students interpret networks and network diagrams used to represent relationships in practical situations and describe connectedness. AC9M10SP02
  • Students use mathematical modelling to solve applied problems involving growth and decay, including financial contexts; formulate problems, choosing to apply linear, quadratic or exponential models; interpret solutions in terms of the situation; evaluate and modify models as necessary and report assumptions, methods and findings. AC9M10A04

General capabilities

Numeracy

  • Number patterns and algebraic thinking (Level 9)

Critical and creative thinking

  • Consider alternatives (Level 6)
  • Identify, process and evaluate information (Level 6)
  • Interpret concepts and problems (Level 6)
  • Draw conclusions and provide reasons (Level 6)
  • Have students communicate their findings back to the class if time allows and encourage discussion and feedback from the class.
  • Collect students’ Activity 2 worksheets to review and provide feedback.

Prior to this lesson, it is assumed that students have some knowledge of:

  • basic spreadsheet functionality including cell referencing and performing calculations using symbols such as = * and /
  • personal experience or understanding of the airline business, although no specialist knowledge is assumed
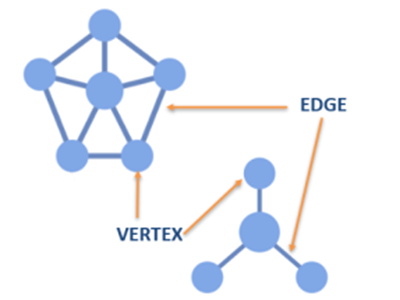
  • language important for this lesson including node, vertex, edge, connected network, degree.
  • Some students have limited knowledge about the airline industry and struggle to identify potential model inputs and variables – use slide 5 from the teacher’s slides as a stimulus with questioning, for example: ‘Why do you think it would be useful to know what routes competitors fly and what they charge?’
  • Students may believe that network maps must accurately reflect the position of people, places and things – refer to local examples such as train and bus maps or circuit diagrams that are not drawn to scale and discuss why this is the case.
  • Some students have gaps in spreadsheet skills or knowledge – explicitly demonstrate and explain the key features and operation of spreadsheets. Use the provided Excel model and encourage students to interrogate formulae in cells to understand how the calculations have been derived. For students creating their own models, encourage use of online help videos.

What you need:

  • Lesson Plan (Word)

  • Teacher's slides (PowerPoint)

  • Capital Airways Activity 2 (Word)

  • Capital Airways spreadsheet (Excel)

  • Laptops or other devices with spreadsheet package available.

Learning goals

Learning intention

  • We are learning the key language associated with networks.
  • We are learning to understand how to create and interpret network diagrams.
  • We will learn the complexities in building mathematical models and begin to tackle a modelling problem.

Success criteria

By the end of this lesson, students can:

  • name and describe the key features of a network diagram
  • interpret a network diagram to answer practical problems
  • amend or create a network diagram to meet specific criteria
  • use or build a mathematical model in a spreadsheet to optimise financial outcomes.

Why are we learning about this?

Creating, interpreting and manipulating network diagrams is a skill set applicable in logistics, computer science and social sciences. Delving into the complexities of mathematical modelling, equips us to use or build a spreadsheet model to optimise financial outcomes. This provides practical problem-solving tools for real-world scenarios with many business applications.

Learning hook 10 mins

Introduction

In this lesson (Part 2), students conduct a mathematical investigation on networks.

Download the teacher’s slides that accompany this lesson and begin by reviewing the learnings of Part 1.

(Slide 2) Refer to the network diagrams, key vocabulary and main concepts. If not already done in the previous lesson, go through the solutions to Activity 1 and ensure that all students feel confident to learn further.

Explore 30 mins

Note: Prepare by downloading and printing (or providing a digital copy) Activity 2 (Word) and the Capital Airways spreadsheet (Excel document) for the class.

Optimising a network and creating network diagrams

  • (Slide 3) Organise students into groups of 3–4 and introduce Activity 2 – Improving the Capital Airways network. Introduce the new scenario.

‘After your tour around the network you realise that Capital is in serious trouble. It can be hard making a profit as an airline and Capital is suffering big losses. Lots of planes are flying half full (or worse) and you are struggling to cover costs. You think that one key way to improve Capital’s fortunes, is to restructure the airline’s route map. You collect your executive team together to implement your plan. Your idea is to build a detailed mathematical model to calculate the profit flying different routes to try and optimise the route map and return Capital to profitability.’

  • Ask groups to brainstorm a list of information they need to know to build their model and make decisions about routes and pricing.
  • (Slide 4) Collect a range of suggestions from the different groups and compare these with this pre-prepared list of possible inputs and variables, clarifying the rationale or the effect on using different inputs and variables. Note that many mathematical models, such as those that predict future climates, can contain literally hundreds of variables, but clearly these are highly complex to build and to understand.
  • (Slide 5) Now introduce the simplified modelling task as detailed here:

‘Assume Capital Airways can fly any 10 routes in the network (that is, connecting any pair of capitals), but the final route map must allow travel between all capitals. There are 10 planes in the Capital fleet: 5 Boeing 737-Max 7 planes (140 passengers); 5 Airbus 321 Neos (220 passengers).

  1. Use the information provided on passenger numbers and the population of each capital to determine your routes and which plane will fly each route.
  2. Build a mathematical model calculating the total daily profit from your route network.
  3. Create two revised network maps (on the maps provided) showing your chosen routes, projected daily passenger numbers on each route and projected daily profit on each route.
  4. Summarise the key points of your route map in 5 bullet points to be presented to the Capital Airways Board.’
  • (Slide 6) Explain the key steps and model inputs that the students need to determine:

Decide your routes and note the current passenger numbers on each route. For each route you must:

  • choose the plane you will use, how full you estimate it will be (% capacity) and ticket price
  • Remember that as you increase price, capacity will fall. You will need to consider ticket prices charged by competitors as well as demand on the route (current passenger numbers)
  • calculate fuel cost, by finding the route distance and entering it into the model, which will then automatically calculate the daily fuel cost
  • calculate the ground staff and airport fees, which are calculated per passenger but vary for larger versus smaller airports.
  • As you vary inputs (blue cells) to the model, the revenue, costs and profit will update, allowing you to test different assumptions.

It may be helpful at this stage to project the Excel model and explore the tabs containing additional information, which may also be downloaded and distributed to students. Explain the input protocol – blue cells are inputs, green cells auto-populate based on previous inputs, white cells are calculations. Explore the calculations underpinning the example Adelaide to Brisbane route. Students should then work in their groups to complete the task with the teacher monitoring progress.

Summary and reflection 15 mins

Use this time as a combined formative assessment opportunity to lead a discussion on groups’ findings. Ask how the groups found Activity 2 ­ what they found difficult, or easy or any interesting things they noted during their investigations.