Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
The product of squares
Throughout this inquiry students will make connections, test different cases, infer and explain rules. They will evaluate the relationship between base and index numbers and square numbers. Students multiply index numbers, being familar with index laws and rules. Students are provided with worked examples. Teachers can use the inquiry as a teaching tool and to provide similar equations for students to work through and explain their findings. Resources include a prompt sheet and PowerPoint presentation.
Additional details |
|
| Year level(s) | Year 7, Year 8 |
|---|---|
| Audience | Student, Teacher |
| Purpose | Additional learning support, Assessment advice, Content knowledge, Evidence-based approaches, Extension, Teaching resource, Teaching strategies, Student task |
| Format | Downloadable resources |
| Teaching strategies and pedagogical approaches | Collaborative learning, Differentiated teaching, Explicit teaching, Feedback, Growth mindset, Mathematics investigation, Metacognitive strategies, Questioning, Worked examples, Structuring lessons |
| Keywords | laws of indices, square root, whole number, positive indices, powers of, base and index numbers, square numbers, explicit teaching |
Curriculum alignment |
|
| Curriculum connections | Critical and creative thinking, Numeracy |
| Strand and focus | Number, Algebra, Apply understanding, Build understanding |
| Topics | Addition and subtraction, Indices, Multiples, factors and powers, Operating with number |
| AC: Mathematics (V9.0) content descriptions |
AC9M7N01
Describe the relationship between perfect square numbers and square roots, and use squares of numbers and square roots of perfect square numbers to solve problems
AC9M8N02
Establish and apply the exponent laws with positive integer exponents and the zero-exponent, using exponent notation with numbers |
| Numeracy progression |
Multiplicative strategies (P9)
|
Copyright details |
|
| Organisation | Inquiry Maths |
| Copyright | © Andrew Blair 2012-21. Creative Commons BY-NC-SA 4.0. |
Related resources
-

Adding fractions
Solving problems involving addition and subtraction of fractions, including those with unrelated denominators.
Resource details -
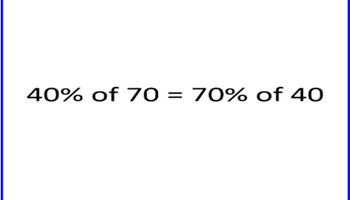
Percentage of
Find percentages of quantities and express one quantity as a percentage of another.
Resource details -

Laws of arithmetic
Extend and apply the laws and properties of arithmetic to algebraic terms and expressions.
Resource details -
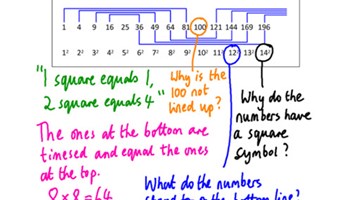
Index patterns
These lessons involve the use of number lines to build understanding of exponents both negative and postive.
Resource details
