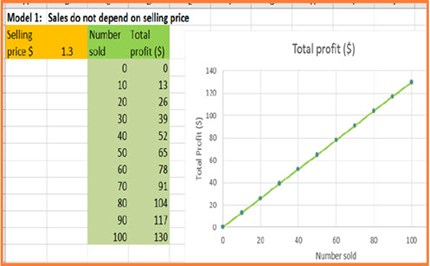
reSolve: Mathematical modelling – Pricing for profit

In this unit, students approach the problem of how to price a product to maximise profit, in this case, items sold at a school fair to raise money. The unit involves students in iterative cycles of model improvement as they consider more sophisticated versions. As they work through the unit, students see how varying the assumptions that they make affects the mathematical model they develop.

Additional details
Year level(s)	Year 8
Audience	Teacher
Purpose	Teaching resource
Teaching strategies and pedagogical approaches	Mathematics investigation
Keywords	modelling, profit
Curriculum alignment
Curriculum connections	Numeracy
Strand and focus	Algebra, Apply understanding
Topics	Linear relationships, Non-linear relationships, Money and financial mathematics
AC: Mathematics (V9.0) content descriptions	AC9M8A02 Graph linear relations on the Cartesian plane using digital tools where appropriate; solve linear equations and one-variable inequalities using graphical and algebraic techniques; verify solutions by substitution AC9M8N05 Use mathematical modelling to solve practical problems involving rational numbers and percentages, including financial contexts; formulate problems, choosing efficient calculation strategies and using digital tools where appropriate; interpret and communicate solutions in terms of the situation, reviewing the appropriateness of the model
Numeracy progression	Number patterns and algebraic thinking (P7) Proportional thinking (P6) Understanding money (P8)
Copyright details
Organisation	ReSolve: Maths by Inquiry
Copyright	© Australian Government Department of Education, Skills and Employment 2021. Creative Commons BY-NC-SA 4.0.