Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
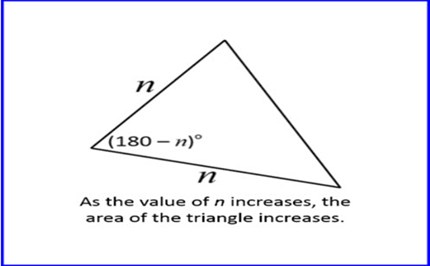
Area of a triangle
The prompt will challenge students to think about the area of a non-right-angled triangle, using the general sine formula. They also explore the concept of proof, deepening their conceptual understanding. The resource includes classroom examples, teacher notes and guided questions.
Additional details |
|
| Year level(s) | Year 9, Year 10 |
|---|---|
| Audience | Teacher |
| Purpose | Assessment task, Extension, Student task, Teaching resource |
| Format | Downloadable resources |
| Teaching strategies and pedagogical approaches | Collaborative learning, Differentiated teaching, Explicit teaching, Feedback, Mathematics investigation |
| Keywords | sine, triangle, angle, proof, area |
Curriculum alignment |
|
| Curriculum connections | Critical and creative thinking, Numeracy |
| Strand and focus | Space, Measurement, Algebra, Apply understanding, Build understanding |
| Topics | Algebraic expressions, Angles and geometric reasoning |
| AC: Mathematics (V9.0) content descriptions |
AC9M9SP01
Recognise the constancy of the sine, cosine and tangent ratios for a given angle in right-angled triangles using properties of similarity
AC9M10M03
Solve practical problems applying Pythagoras' theorem and trigonometry of right-angled triangles, including problems involving direction and angles of elevation and depression |
| Numeracy progression |
Proportional thinking (P7)
Understanding geometric properties (P7) Understanding units of measurement (P10) |
Copyright details |
|
| Organisation | Inquiry Maths |
| Copyright | © Andrew Blair 2012-21. Creative Commons BY-NC-SA 4.0. |
Related resources
-

Three points on a circle
This prompt will challenge students to explore their understanding of the equation of a circle.
Resource details -
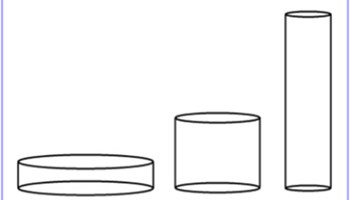
Volume of a cylinder
This prompt will challenge students to explore their understanding of integers and the volume of cylinders.
Resource details -

Intersecting lines
Using this prompt will encourage students to apply their knowledge of linear equations and intersecting lines. It leads into simultaneous equations.
Resource details -
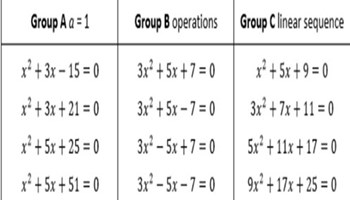
Odd coefficients
This prompt will challenge students to think about the structure of a quadratic equation.
Resource details