Please note: This site contains links to websites not controlled by the Australian Government or ESA. More information here.
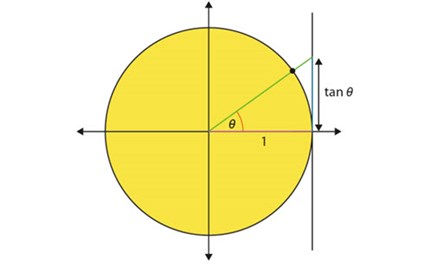
3.2 Trigonometry
This paper introduces trigonometry by breaking it into two sections:
- Understanding trigonometric functions
- Using trigonometry to solve problems in context.
It provides details of the knowledge students should have and some of the misconceptions they may hold. Examples are given to illustrate what these misconceptions may look like, how to address them, and support teachers in developing pedagogical and content knowledge.
Additional details |
|
| Year level(s) | Year 9, Year 10 |
|---|---|
| Audience | Teacher, School Leader |
| Purpose | Content knowledge |
| Format | Downloadable resources |
| Keywords | Trigonometry, ratio, sine, cosine, tangent |
Curriculum alignment |
|
| Strand and focus | Space |
| Topics | Pythagoras and trigonometry |
| AC: Mathematics (V9.0) content descriptions |
AC9M9SP02
Apply the enlargement transformation to shapes and objects using dynamic geometry software as appropriate; identify and explain aspects that remain the same and those that change
AC9M9M03
Solve spatial problems, applying angle properties, scale, similarity, Pythagoras' theorem and trigonometry in right-angled triangles
AC9M10M03
Solve practical problems applying Pythagoras' theorem and trigonometry of right-angled triangles, including problems involving direction and angles of elevation and depression |
| Numeracy progression |
Understanding geometric properties (P7)
Proportional thinking (P7) Understanding units of measurement (P10) |
Copyright details |
|
| Organisation | NCETM |
| Copyright | © Crown Copyright. Free-for-education material. |
Related resources
-
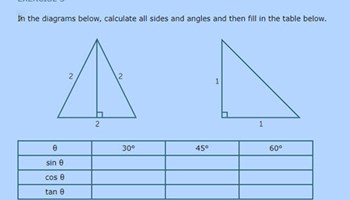
Introductory trigonometry
Introducing trigonometrical ratios and their uses
Resource details -
Proof
A series of articles on the history and different types of proof.
Resource details -

Types of mathematical proof
An article on the different types of mathematical proof.
Resource details -

Misunderstandings
A number of articles and activities that address misconceptions and misunderstandings about mathematical proof students may have, given this is a difficult concept.
Resource details